In this article, I will address one of the questions that I have recently been asked. It is on the topic of huge swings in the implied volatility on an individual stock. In order to get to the bottom of the issue under discussion, I have utilized the CBOE's Option Calculator. Here is the question that I was asked:
I own a biotech stock that is currently trading around $50 and I have recently sold some 55 strike covered calls with the expiration next month. The very next day, out of nowhere, positive news came out and the stock jumped $3. However, the value of the option fell by nearly 30%. How can that be?
The simple answer to your question is that the implied volatility decreased, which in turn has caused the premium of your 55 call to decrease as well. I am glad that the price did not rally above your sold 55 call, which could still happen. There is a possibility that within the next month or so, your stock could lift an additional two points which would then make your sold 55 OTM (out-of-the-money) calls in-the-money (ITM). In that case, you need to make a choice whether you still want to keep the stock, or let it get called away from you. The choice is entirely yours.
Now let me address the issue of "How can that be?" in greater detail. We discourage trading pharmaceutical stocks just because of the high volatility shift that can take place for various reasons. For instance, prior to a major announcement, the implied volatility of these stocks (Pharmaceutical or Biotech) could get up to extreme levels. Yet, after the announcement, volatility usually comes back to the stock's normal trading range. It's quite common for novice traders to underestimate the impact of a change in volatility.
Taking into account that the value of the option premium fell by 30%, I would assume that the implied volatility was 80% before the announcement and 50% afterwards. To ensure that this assumption is NOT without quantification, let me run some calculations using the options calculator from the CBOE website.
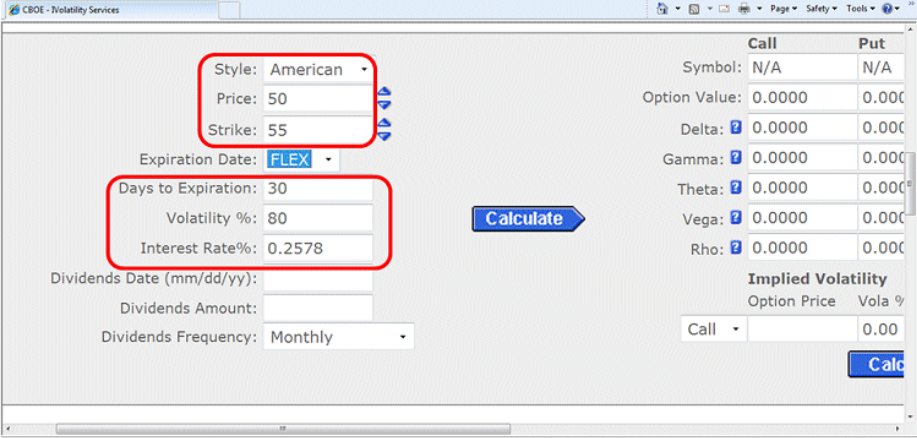
What I have done in the figure above is basically entered the info that I was given. Line by line the entered info is the following: For the Style (of options), I have kept it on the default setting meaning American, for the Price I have entered $50, and for the Strike $55. The Expiration Date/Days to Expiry, I entered 30 days, for that is what the person asking the question had said. Volatility is something that I have entered on my own choosing, while the Interest Rate% was defaulted to 0.2578 due to Mr. Ben B. I have left blank the places for dividends. Once this info was entered, I clicked on Calculate and Figure 2 shows what the premium and the Greeks came out for the 55 call.
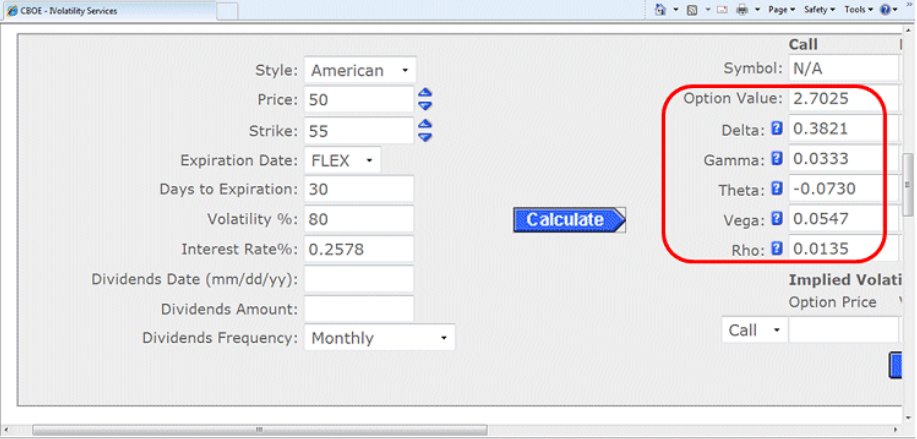
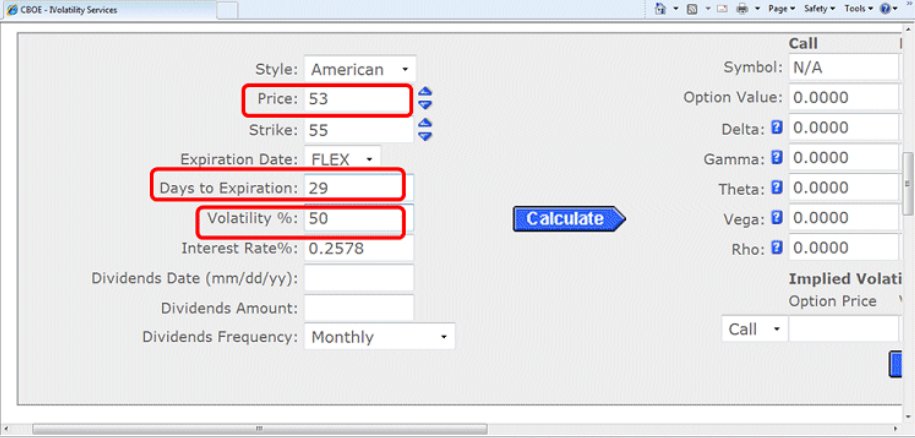
To recap the info from above, the 55 call premium of the OTM option with 30 days to expiry and the IV of 80% should be priced $2.70 with a delta of .38 cents. (For simplicity's sake, I will not go through the rest of the Greeks.) After knowing these facts, let us change the variable in the option calculator by changing the data in the following way. First, the Price should be changed to $53, Days to Expiry decreased by one, and IV dropped by 30%. Figure 3 shows those changes.
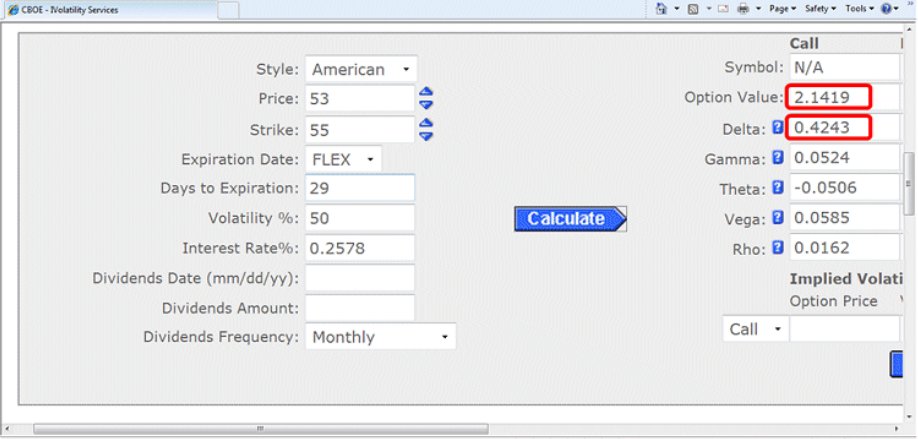
Again, after pressing CALCULATE, the new results for the 55 call were: Option Value or premium of the 55 call at $2.14 with a delta of 0.42.
Now, take a moment and just think about the impact of changes in volatility on trading options. Had the IV remained at the same level (80%) and the stock had rallied 3 points, this is how the incremental increase of the delta for that 55 call would look like.
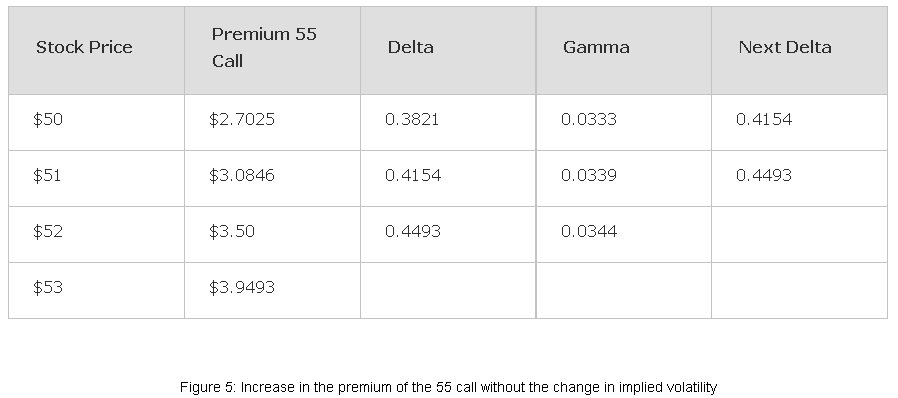
Increase in the premium of the 55 call without the change in implied volatility
At $50 the 55 call is still worth $2.70 yet when the stock lifts to $53, within a day, the 55 call should be worth almost four dollars, ($3.9493 to be exact). However, none of that happened because the IV dropped 30% reducing the premium of the 55 call, which originally was $2.70 with the underlying sitting at $50, to a mere $2.14, while the underlying is at $53.
In conclusion, the decline from $2.70 to $2.14 took place even though the stock price increased three whole points from $50 to $53. The impact of the change in implied volatility easily outweighed the price change of the stock. In short, it is crucial to understand the impact that changes in volatility have on options.
Know your Greeks and have Green Trading.
I own a biotech stock that is currently trading around $50 and I have recently sold some 55 strike covered calls with the expiration next month. The very next day, out of nowhere, positive news came out and the stock jumped $3. However, the value of the option fell by nearly 30%. How can that be?
The simple answer to your question is that the implied volatility decreased, which in turn has caused the premium of your 55 call to decrease as well. I am glad that the price did not rally above your sold 55 call, which could still happen. There is a possibility that within the next month or so, your stock could lift an additional two points which would then make your sold 55 OTM (out-of-the-money) calls in-the-money (ITM). In that case, you need to make a choice whether you still want to keep the stock, or let it get called away from you. The choice is entirely yours.
Now let me address the issue of "How can that be?" in greater detail. We discourage trading pharmaceutical stocks just because of the high volatility shift that can take place for various reasons. For instance, prior to a major announcement, the implied volatility of these stocks (Pharmaceutical or Biotech) could get up to extreme levels. Yet, after the announcement, volatility usually comes back to the stock's normal trading range. It's quite common for novice traders to underestimate the impact of a change in volatility.
Taking into account that the value of the option premium fell by 30%, I would assume that the implied volatility was 80% before the announcement and 50% afterwards. To ensure that this assumption is NOT without quantification, let me run some calculations using the options calculator from the CBOE website.

What I have done in the figure above is basically entered the info that I was given. Line by line the entered info is the following: For the Style (of options), I have kept it on the default setting meaning American, for the Price I have entered $50, and for the Strike $55. The Expiration Date/Days to Expiry, I entered 30 days, for that is what the person asking the question had said. Volatility is something that I have entered on my own choosing, while the Interest Rate% was defaulted to 0.2578 due to Mr. Ben B. I have left blank the places for dividends. Once this info was entered, I clicked on Calculate and Figure 2 shows what the premium and the Greeks came out for the 55 call.

To recap the info from above, the 55 call premium of the OTM option with 30 days to expiry and the IV of 80% should be priced $2.70 with a delta of .38 cents. (For simplicity's sake, I will not go through the rest of the Greeks.) After knowing these facts, let us change the variable in the option calculator by changing the data in the following way. First, the Price should be changed to $53, Days to Expiry decreased by one, and IV dropped by 30%. Figure 3 shows those changes.

Again, after pressing CALCULATE, the new results for the 55 call were: Option Value or premium of the 55 call at $2.14 with a delta of 0.42.

Now, take a moment and just think about the impact of changes in volatility on trading options. Had the IV remained at the same level (80%) and the stock had rallied 3 points, this is how the incremental increase of the delta for that 55 call would look like.

Increase in the premium of the 55 call without the change in implied volatility
At $50 the 55 call is still worth $2.70 yet when the stock lifts to $53, within a day, the 55 call should be worth almost four dollars, ($3.9493 to be exact). However, none of that happened because the IV dropped 30% reducing the premium of the 55 call, which originally was $2.70 with the underlying sitting at $50, to a mere $2.14, while the underlying is at $53.
In conclusion, the decline from $2.70 to $2.14 took place even though the stock price increased three whole points from $50 to $53. The impact of the change in implied volatility easily outweighed the price change of the stock. In short, it is crucial to understand the impact that changes in volatility have on options.
Know your Greeks and have Green Trading.
Last edited by a moderator:
