xxx32 & xxx64 on YM

[blackcab]

Chartman and others talk about xxx32 and xxx64 being significant numbers on YM, eg 10532. I tested this on some 2003 data and didn't find anything unusual about those numbers, but did find something else odd. Maybe I made a mistake, but I can't see it.

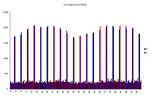
I counted the no. of times each least significant digit pair (00, 01 ... 99) occured over the high and low prices for each bar (57,046 bars in total). I ignored open/close as H/L must be more relevant for 1-minute bars.

The first graph shows the frequency of all the pairs from 00 to 99. What would you expect to see? Fairly flat, maybe with the main round numbers like 00 and 50 occuring a bit more frequently and, if the theory's correct, 32 and 64 being more frequent? But it's nothing like that - the distribution is - well - odd. Each fifth pair (03, 08, 13, 18, 23 ...) occurs much more frequently. Can anyone explain it?

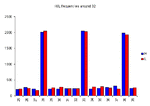
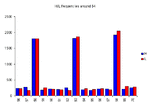
The 2nd and 3rd graphs zoom in to show the frequency of 32 and 64 compared with their neighbours, and there's no difference. that must mean 32/64 are not special after all, i.e. they account for no more bar highs/lows than any other number.

The data I used was YM 1-minute bars from 2.1.03 to 24.7.03, between 8:21 and 15:59 Chicago time - 57,046 bars in total. The price range over the period was 7418-9342. Method in Excel: for each bar's H & L: a=TEXT(price,0); b=RIGHT(a,2); c=VALUE(b); count frequencies of 0-99 inclusive in c.

 

[FetteredChinos]

hmm, could you attach a zip file of the excel data?

it does look intriguingly menthol.

perhaps there is a data issue? or something to do with the way it is collated?

odd.

fc

 

[blackcab]

hmm, could you attach a zip file of the excel data?

it does look intriguingly menthol.

perhaps there is a data issue? or something to do with the way it is collated?

odd.

fc

Here it is cut down to 200 bars, but even that shows the same oddness. Must be an error somewhere.

 

[Bigbusiness]

I think the 32 and 64 that Chartman talks about is on the Dow 30 cash chart. The YM prices are different and vary from the cash throughout the contract period. The YM is valued at about 30 points above the cash price today. Can you do the same work with Dow 30 cash prices?

 

[blackcab]

I've only got YM prices. If Dow 30 cash is a spreadbetting thing I'd guess no-one would have the data.

Can anyone with historical 1m YM data that's not from Disk Trading try it out to see if DT's data is the problem?

 

[rossored]

Unless you can get hold of a load of INDU-I-NYSE data.

I'd offer some up here... if only I had some.

 

[Bigbusiness]

This is a link to a large zip file(6mb) of 1 min DJIA data on page 2 of the 'data' section here www.traders2traders.com

It is too big to open it all in excel but it can be opened in word and split in to years.

 

[blackcab]

It seems the Disk Trading data from tick up to 60 mins has 3-4 times as many YM prices ending in 3 or 8 than it should do. That traders2traders data and T&S straight from CBOT show what you'd expect - no odd spikes.

Bugger.

 

[blackcab]

To follow this up:

Disk Trading advertise their YM data as running from 6/03. When I bought it however they threw in a load of extra data including YM pre-6/03, which was gathered in a quite different way. I lumped all the data together and found those last-digit errors. Having looked at it, all the intraday data up to 15.6.03 is last-digit-skewed and all the data from 16.6.03 is good.

So I was finding errors in data I'd got for free and which wasn't advertised as the 'real' YM data anyway -- all the stuff I'd paid for was fine.

Just in case anyone else has bought YM data from Disk Trading as it will affect you if you do any analysis on it and don't take the pre/post-16.6.03 thing into account.