Simple Moving Averages are a subset of FIR Filters. Exponential Moving Averages are a subset of IIR filters. Traders are not necessarily limited to the selection of one or the other. This article describes how you can make hybrid filters and realized the best characteristics of both.
Many traders have come to me, asking me to make their indicators act just one day sooner. They are convinced that this is just the edge they need to make a zillion dollars. While their profit expectation may not be realized, it is true that lag is the downfall of many trading systems. If you want to shorten the lag of your indicators, or if you want to get more smoothing from your filters, the techniques in this article may be just what you have been seeking. Rather than creating the indicators, I will show you ways to make your own techniques better by improving their filters. Filters are part of almost every indicator.
There are two fundamentally different kinds of filters, Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. Simple Moving Average (SMA) and Weighted Moving Average (WMA) filters are examples of FIR filters and an Exponential Moving Average (EMA) is an example of an IIR filter.
An impulse can be pictured as data that has a value of one at only one bar and is zero everywhere else. When this data is a applied to a five bar simple moving average, for example, the output of the moving average is zero until the impulse enters the input of the filter. Then the output is one-fifth, the input averaged across the width of the filter. As time progresses, the filter output remains one-fifth when the impulse is positioned at the second, third, fourth, and fifth position of the moving average. Finally, the impulse falls outside the moving average and the filter output becomes zero, and remains zero for the rest of the data set. Thus, the response to the impulse input is finite in duration - it only lasts as long as the impulse is within the filter length. This is why it is so named FIR. The output of the Simple Moving Average is plotted with respect to the right hand side of the filter on our charts. However, the average position is at (N-1)/2 for an N bar moving average. The difference between where the average is plotted and its average position is the lag of the filter. Thus, a 5 bar Simple Moving Average will have a 2 bar lag.
A Weighted Moving Average (WMA) is another example of a FIR filter. In a WMA, the oldest data has a weight of one, the next oldest has a weight of two, and so on, until the most recent data has a weight of N for an N-length WMA. When an impulse is applied to the input of a WMA the output is a scaled replica of the weighting function. The weighting is in the shape of a triangle, with the result that the lag is the "center of gravity" of the weighting function, or about one-third the length of the filter. The lag can be calculated as (N-1)/3 for an N-Bar WMA. Therefore, a 4 bar WMA has a lag of only one bar, a 7 bar WMA has a lag of 2 bars, and so on.
IIR filters are fundamentally different from FIR filters because a recursive calculation is employed, using the results of a previous calculation. The equation to compute an EMA is
In English, this equation says that the current EMA value is equal to a fraction of the current price plus the quantity one minus that fraction, the quantity times the previous EMA value. If the Price is an impulse, the first output value of the EMA is because there is no previous filter output value. The next output value is *(1-) because there is no new input and the previous calculation value was . Then, the next output value is *(1-)2. The following output value is *(1-)3, and so on. The sequence continues, so that the Nth output value is *(1-)N. The output value decreases as the exponent of the sample number, hence the name Exponential Moving Average. Regardless of how many samples have occurred since the impulse event, there is theoretically some contribution of the impulse present in the output. That makes the EMA an Infinite Impulse Response filter. It can be shown that the alpha term in an EMA can be computed to provide the equivalent smoothing of a SMA as
Since the lag produced by a SMA is approximately half the filter length, it also can be shown that the alpha of an EMA can be computed from the amount of allowed lag as
From these equations, it can be seen that an EMA having = .33 is equivalent to a five bar SMA or a 7 bar WMA (the lag of a 7 bar WMA being 2 bars).
Let's examine the performance of some of these filters. The prices are sampled data, and information theory says that we must have at least two samples per cycle of the highest frequency being considered. This highest frequency is called the Nyquist frequency, and is a 2 bar cycle. Generalized frequency responses are normalized so that the Nyquist frequency is one. With this normalization, a four bar cycle has a normalized frequency of 2/4= 0.5 and a 20 bar cycle has a normalized frequency of 2/20=0.1, and so on. To observe the amplitude response of the filters, the output is scaled in decibels (dB). A decibel is ten times the log of the power ratio. Therefore half power is -3 dB and one-tenth power is -10 dB. It should also be noted that power is proportional to the square of the wave amplitude. With these definitions, we see the response of a four bar SMA in Figure 1. One 4-bar cycle exactly fits in the 4-bar SMA. One fully cycle averages to zero, so we see a notch in the response at the 0.5 normalized frequency. There are two 2-bar cycles that exactly fit within the 4-bar SMA. These two cycles also average to zero, producing the notch at the 1.0 normalized frequency. Incidentally, all even-order symmetrical FIR filters always produce a notch for the 2 bar cycle (Nyquist frequency = 1). For this reason, even order (2, 4, 8, 10, etc.) symmetrical FIR filters are preferred over odd order FIR filters.
One FIR filter of interest to traders is a 6th order filter whose coefficients are symmetrically weighted as [.0833 .1667 .25 .25 .1667 .0933]. The response of this filter, shown in Figure 2, has a notch for 2, 3, and 4 bar cycles. This filter has a lag of 2.5 bars for all frequencies.
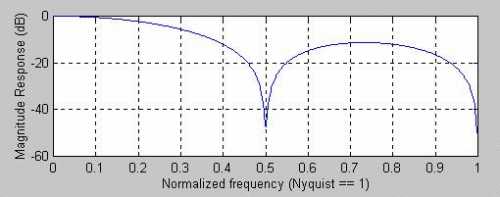
caption: Figure 1. Frequency Response of a 4 Bar SMA.
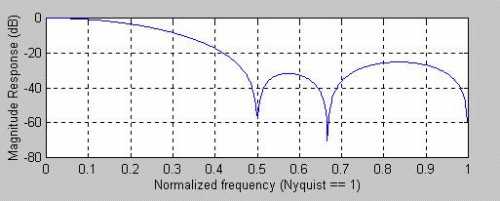
caption: Figure 2. Frequency Response of a 6th Order FIR filter notches 2, 3, and 4 bar cycles.
All FIR filters do not need to have symmetrically distributed coefficients. For example, the coefficients of a 4-bar WMA are [4 3 2 1]/10. The delay of a 4-bar WMA is only 1 bar at all frequencies and its frequency response is shown in Figure 3. Clearly, there are no notches because of the asymmetrical coefficient weighting. Additional smoothing can be obtained by increasing the length of the filter. For example, a 7-bar WMA frequency response is shown in Figure 4. The lag of a 7-bar WMA is 2 bars at all frequencies.
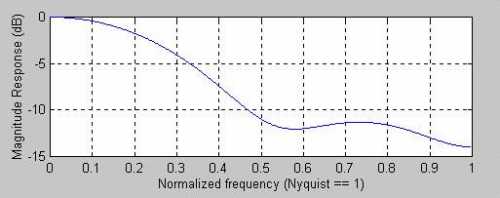
caption: Figure 3. Frequency Response of a 4-bar WMA.
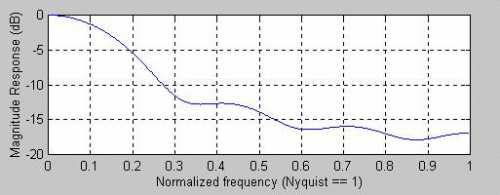
caption: Figure 4. Frequency Response of a 7-bar WMA.
The responses of these FIR filters can be contrasted to the response of an IIR filter. For example, and EMA that has a 2-bar low frequency lag has the frequency response shown in Figure 5. Comparing Figure 5 to Figure 4 we see that the 7-bar WMA has marginally better smoothing than the 5-bar EMA. The real difference between these filters is in their lag characteristics. While the 7-bar WMA has a 2-bar lag at all frequencies, the lag of the 5-bar EMA is shown in Figure 6. The low frequency lag is 2 bars, but this lag quickly decreases so the frequencies whose period are shorter than about 8 bars have a modest lead. This really is inconsequential because these shorter cycles have been reduced in amplitude by the filter.
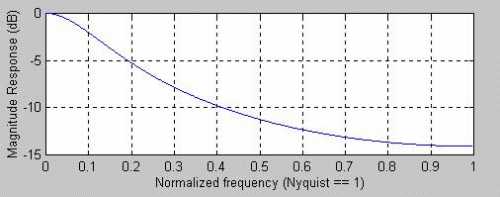
caption: Figure 5. Frequency Response of a 5-bar EMA.
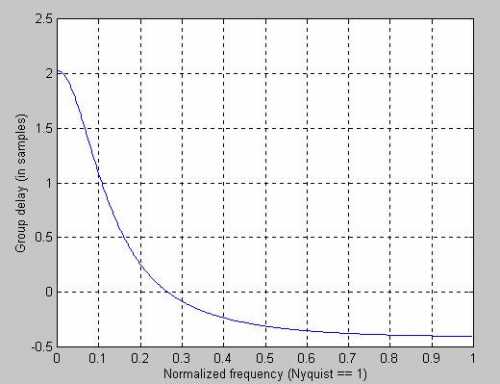
caption: Figure 6. Lag of a 5-bar EMA.
The discussion of the responses of FIR and IIR filters were just precursors to the discussion of the hybrid FIR-IIR filters I propose. This is because we must understand the components before we can appreciate the benefits of the hybrid. Recalling the equation for an EMA, there is no reason we cannot modify it to be
This simple change constitutes one of our hybrid filters. All we did was insert the WMA for Price in the EMA equation. If we insert a 4-bar WMA in a 5-bar EMA we get the frequency response shown in Figure 7. Its lag is shown in Figure 8. Wow! We get a ton of additional smoothing for the minor price of only one additional bar of low frequency lag, compared to standard EMA.
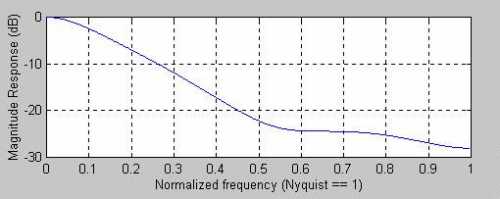
caption: Figure 7. Frequency Response of Hybrid 4-bar WMA and 5-bar EMA filter.
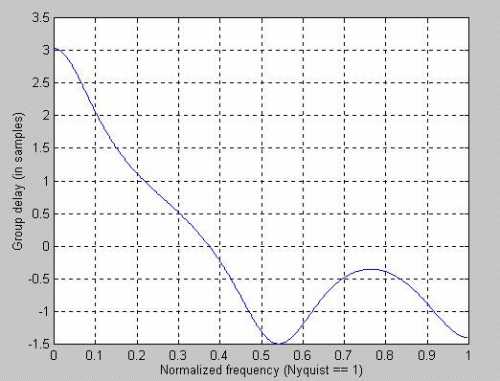
caption: Figure 8. Lag of Hybrid 4-bar WMA and 5-bar EMA filter.
While it's well and good that we can get additional smoothing from our Hybrid filter, let's return to the original premise that the filter lag can be reduced. One way of reducing lag is adding the slope of prices to the current price. This is like making a prediction of future prices if the rate of change continues. If we add a 1-bar momentum to the current price, this is like making a 1-bar prediction. The equation looks like
This is a kind of FIR filter, and this filter has a 1-bar lead instead of a lag. The frequency response of this FIR filter is shown in Figure 9. Whoa! Not only do we not have smoothing, but the higher frequency components are actually amplified. A 2-bar cycle is amplified by nearly 10 dB. This amplification is why predictive filters are seldom successful - the amplified high frequency components make the prediction so erratic that the prediction is useless.
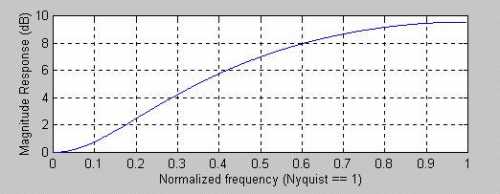
caption: Figure 9. Frequency Response of a Predictive FIR filter
Now, lets examine what happens when we create a Hybrid filter as
The FIR part of the Hybrid filter has a 1-bar lead at all frequencies and the IIR part of the filter has a 2 bar low frequency lag. Our guess is that we should expect a 1-bar lag low frequency component and perhaps some lead at higher frequencies. But first, let's examine the frequency response behavior of this Hybrid filter. Its frequency response is shown in Figure 10. While the smoothing obtained by this filter is modest, at least it does not amplify the higher frequency components. The lag of the filter, shown in Figure 11, has the expected 1-bar lag at low frequencies and quickly drops to near zero across most of the frequency band.
{$image10 caption="Figure 10. Frequency Response of a Zero Lag Hybrid Filter."
{$image11 caption="Figure 11. Lag Response of a Zero Lag Hybrid Filter."
The Hybrid filter examples I have shown have either produced a substantial increase in smoothing at a modest cost of delay or have substantially reduced lag while continuing to provide some smoothing. The formulation of these Hybrid filters is simple and the combinations are endless. I hope you can find a Hybrid filter combination you can use to advantage in your own trading. Now that you know how to reduce lag by one bar, you too can make a zillion dollars.
Many traders have come to me, asking me to make their indicators act just one day sooner. They are convinced that this is just the edge they need to make a zillion dollars. While their profit expectation may not be realized, it is true that lag is the downfall of many trading systems. If you want to shorten the lag of your indicators, or if you want to get more smoothing from your filters, the techniques in this article may be just what you have been seeking. Rather than creating the indicators, I will show you ways to make your own techniques better by improving their filters. Filters are part of almost every indicator.
There are two fundamentally different kinds of filters, Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. Simple Moving Average (SMA) and Weighted Moving Average (WMA) filters are examples of FIR filters and an Exponential Moving Average (EMA) is an example of an IIR filter.
An impulse can be pictured as data that has a value of one at only one bar and is zero everywhere else. When this data is a applied to a five bar simple moving average, for example, the output of the moving average is zero until the impulse enters the input of the filter. Then the output is one-fifth, the input averaged across the width of the filter. As time progresses, the filter output remains one-fifth when the impulse is positioned at the second, third, fourth, and fifth position of the moving average. Finally, the impulse falls outside the moving average and the filter output becomes zero, and remains zero for the rest of the data set. Thus, the response to the impulse input is finite in duration - it only lasts as long as the impulse is within the filter length. This is why it is so named FIR. The output of the Simple Moving Average is plotted with respect to the right hand side of the filter on our charts. However, the average position is at (N-1)/2 for an N bar moving average. The difference between where the average is plotted and its average position is the lag of the filter. Thus, a 5 bar Simple Moving Average will have a 2 bar lag.
A Weighted Moving Average (WMA) is another example of a FIR filter. In a WMA, the oldest data has a weight of one, the next oldest has a weight of two, and so on, until the most recent data has a weight of N for an N-length WMA. When an impulse is applied to the input of a WMA the output is a scaled replica of the weighting function. The weighting is in the shape of a triangle, with the result that the lag is the "center of gravity" of the weighting function, or about one-third the length of the filter. The lag can be calculated as (N-1)/3 for an N-Bar WMA. Therefore, a 4 bar WMA has a lag of only one bar, a 7 bar WMA has a lag of 2 bars, and so on.
IIR filters are fundamentally different from FIR filters because a recursive calculation is employed, using the results of a previous calculation. The equation to compute an EMA is
EMA = *Price + (1-)*EMA[1]
Where is a number less than one
In English, this equation says that the current EMA value is equal to a fraction of the current price plus the quantity one minus that fraction, the quantity times the previous EMA value. If the Price is an impulse, the first output value of the EMA is because there is no previous filter output value. The next output value is *(1-) because there is no new input and the previous calculation value was . Then, the next output value is *(1-)2. The following output value is *(1-)3, and so on. The sequence continues, so that the Nth output value is *(1-)N. The output value decreases as the exponent of the sample number, hence the name Exponential Moving Average. Regardless of how many samples have occurred since the impulse event, there is theoretically some contribution of the impulse present in the output. That makes the EMA an Infinite Impulse Response filter. It can be shown that the alpha term in an EMA can be computed to provide the equivalent smoothing of a SMA as
= 2 / (Length + 1)
Since the lag produced by a SMA is approximately half the filter length, it also can be shown that the alpha of an EMA can be computed from the amount of allowed lag as
= 1 / (Lag + 1)
From these equations, it can be seen that an EMA having = .33 is equivalent to a five bar SMA or a 7 bar WMA (the lag of a 7 bar WMA being 2 bars).
Let's examine the performance of some of these filters. The prices are sampled data, and information theory says that we must have at least two samples per cycle of the highest frequency being considered. This highest frequency is called the Nyquist frequency, and is a 2 bar cycle. Generalized frequency responses are normalized so that the Nyquist frequency is one. With this normalization, a four bar cycle has a normalized frequency of 2/4= 0.5 and a 20 bar cycle has a normalized frequency of 2/20=0.1, and so on. To observe the amplitude response of the filters, the output is scaled in decibels (dB). A decibel is ten times the log of the power ratio. Therefore half power is -3 dB and one-tenth power is -10 dB. It should also be noted that power is proportional to the square of the wave amplitude. With these definitions, we see the response of a four bar SMA in Figure 1. One 4-bar cycle exactly fits in the 4-bar SMA. One fully cycle averages to zero, so we see a notch in the response at the 0.5 normalized frequency. There are two 2-bar cycles that exactly fit within the 4-bar SMA. These two cycles also average to zero, producing the notch at the 1.0 normalized frequency. Incidentally, all even-order symmetrical FIR filters always produce a notch for the 2 bar cycle (Nyquist frequency = 1). For this reason, even order (2, 4, 8, 10, etc.) symmetrical FIR filters are preferred over odd order FIR filters.
One FIR filter of interest to traders is a 6th order filter whose coefficients are symmetrically weighted as [.0833 .1667 .25 .25 .1667 .0933]. The response of this filter, shown in Figure 2, has a notch for 2, 3, and 4 bar cycles. This filter has a lag of 2.5 bars for all frequencies.

caption: Figure 1. Frequency Response of a 4 Bar SMA.

caption: Figure 2. Frequency Response of a 6th Order FIR filter notches 2, 3, and 4 bar cycles.
All FIR filters do not need to have symmetrically distributed coefficients. For example, the coefficients of a 4-bar WMA are [4 3 2 1]/10. The delay of a 4-bar WMA is only 1 bar at all frequencies and its frequency response is shown in Figure 3. Clearly, there are no notches because of the asymmetrical coefficient weighting. Additional smoothing can be obtained by increasing the length of the filter. For example, a 7-bar WMA frequency response is shown in Figure 4. The lag of a 7-bar WMA is 2 bars at all frequencies.

caption: Figure 3. Frequency Response of a 4-bar WMA.

caption: Figure 4. Frequency Response of a 7-bar WMA.
The responses of these FIR filters can be contrasted to the response of an IIR filter. For example, and EMA that has a 2-bar low frequency lag has the frequency response shown in Figure 5. Comparing Figure 5 to Figure 4 we see that the 7-bar WMA has marginally better smoothing than the 5-bar EMA. The real difference between these filters is in their lag characteristics. While the 7-bar WMA has a 2-bar lag at all frequencies, the lag of the 5-bar EMA is shown in Figure 6. The low frequency lag is 2 bars, but this lag quickly decreases so the frequencies whose period are shorter than about 8 bars have a modest lead. This really is inconsequential because these shorter cycles have been reduced in amplitude by the filter.

caption: Figure 5. Frequency Response of a 5-bar EMA.

caption: Figure 6. Lag of a 5-bar EMA.
The discussion of the responses of FIR and IIR filters were just precursors to the discussion of the hybrid FIR-IIR filters I propose. This is because we must understand the components before we can appreciate the benefits of the hybrid. Recalling the equation for an EMA, there is no reason we cannot modify it to be
Hybrid = *WMA + (1-)*Hybrid[1]
This simple change constitutes one of our hybrid filters. All we did was insert the WMA for Price in the EMA equation. If we insert a 4-bar WMA in a 5-bar EMA we get the frequency response shown in Figure 7. Its lag is shown in Figure 8. Wow! We get a ton of additional smoothing for the minor price of only one additional bar of low frequency lag, compared to standard EMA.

caption: Figure 7. Frequency Response of Hybrid 4-bar WMA and 5-bar EMA filter.

caption: Figure 8. Lag of Hybrid 4-bar WMA and 5-bar EMA filter.
While it's well and good that we can get additional smoothing from our Hybrid filter, let's return to the original premise that the filter lag can be reduced. One way of reducing lag is adding the slope of prices to the current price. This is like making a prediction of future prices if the rate of change continues. If we add a 1-bar momentum to the current price, this is like making a 1-bar prediction. The equation looks like
Filt = Price + (Price - Price[1])
= 2*Price - Price[1]
This is a kind of FIR filter, and this filter has a 1-bar lead instead of a lag. The frequency response of this FIR filter is shown in Figure 9. Whoa! Not only do we not have smoothing, but the higher frequency components are actually amplified. A 2-bar cycle is amplified by nearly 10 dB. This amplification is why predictive filters are seldom successful - the amplified high frequency components make the prediction so erratic that the prediction is useless.

caption: Figure 9. Frequency Response of a Predictive FIR filter
Now, lets examine what happens when we create a Hybrid filter as
Hybrid = .33*Filt + .67*Hybrid[1]
The FIR part of the Hybrid filter has a 1-bar lead at all frequencies and the IIR part of the filter has a 2 bar low frequency lag. Our guess is that we should expect a 1-bar lag low frequency component and perhaps some lead at higher frequencies. But first, let's examine the frequency response behavior of this Hybrid filter. Its frequency response is shown in Figure 10. While the smoothing obtained by this filter is modest, at least it does not amplify the higher frequency components. The lag of the filter, shown in Figure 11, has the expected 1-bar lag at low frequencies and quickly drops to near zero across most of the frequency band.
{$image10 caption="Figure 10. Frequency Response of a Zero Lag Hybrid Filter."
{$image11 caption="Figure 11. Lag Response of a Zero Lag Hybrid Filter."
The Hybrid filter examples I have shown have either produced a substantial increase in smoothing at a modest cost of delay or have substantially reduced lag while continuing to provide some smoothing. The formulation of these Hybrid filters is simple and the combinations are endless. I hope you can find a Hybrid filter combination you can use to advantage in your own trading. Now that you know how to reduce lag by one bar, you too can make a zillion dollars.
Last edited by a moderator:
