Why do traders fail?

[neil]

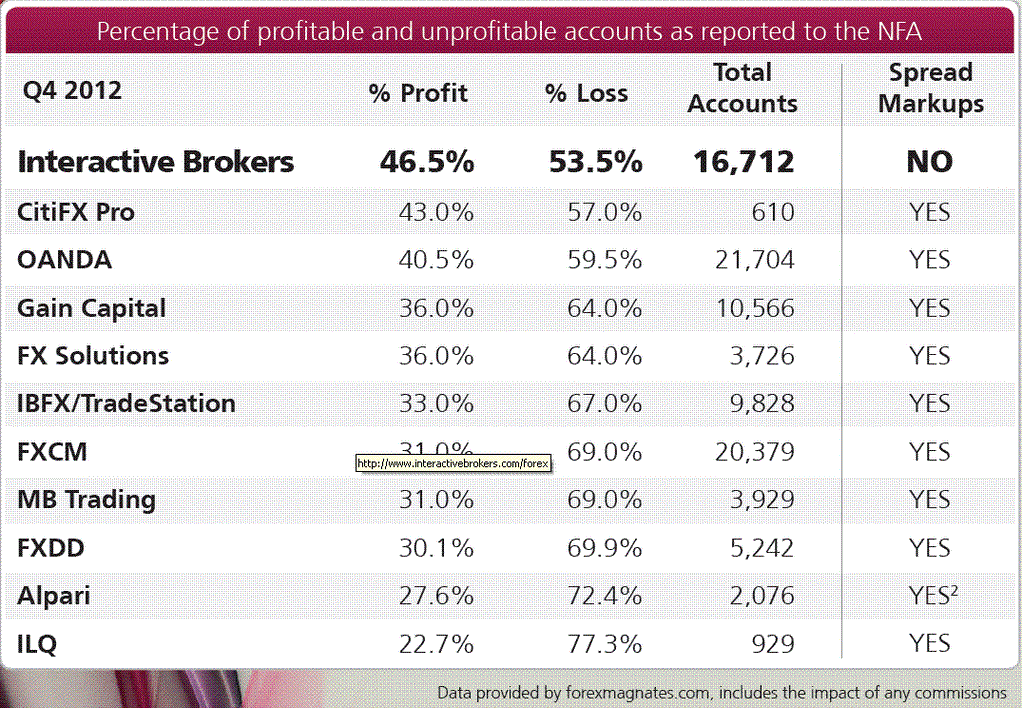
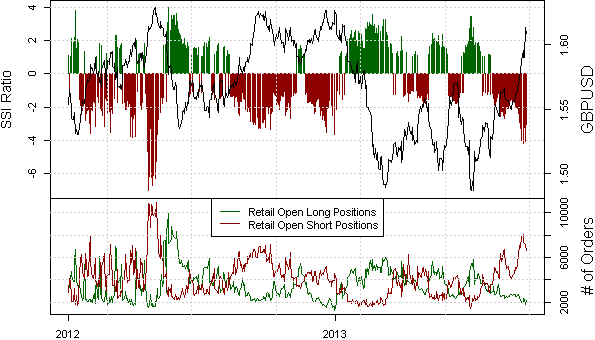
Like you, I was also interested in the disparity in performance between EUR/USD trades and AUD/JPY trades. While this was not something covered in the DailyFX study, I have a few humble theories of my own. First, EUR/USD is the first pair that most people who are new to forex tend to start out trading. People usually don't branch out to trading a pair like AUD/JPY until they have developed their skills and knowledge. Second, AUD/JPY tends to trend nicely, while EUR/USD is choppier. Just look at the two chart below covering the same time frame.

Thanks Jason - that was worth knowing. I think I will keep this one on my watch list

 

[timsk]

. . . EUR/USD is the first pair that most people who are new to forex tend to start out trading. People usually don't branch out to trading a pair like AUD/JPY until they have developed their skills and knowledge. Second, AUD/JPY tends to trend nicely, while EUR/USD is choppier.

Hi Jason.
Many thanks for this. It's really useful stuff and the kind of thing that newbies to T2W wanting to trade forex need to know. This, combined with the stats you've posted thus far offer compelling evidence about risk management, leverage and choice of instrument.

On a separate note, I think I see what Purple Brain is driving at. I may have misunderstood him, but I think the general gist is along the lines of: did the traders who were profitable over the 3 month study period just get lucky and then crash 'n burn soon after, or were they able to repeat their success, indicating that they can take profits on a consistent basis over an extended period of time? I.e., did they just get lucky like the masses of long only equity traders in the run up to the dot com bubble in 2000, or have they acquired genuine lasting skill that enables them to trade in all types of markets - trending, range bound or otherwise!
Cheers,
Tim.

 

[Jason Rogers]

Hi Jason.
Many thanks for this. It's really useful stuff and the kind of thing that newbies to T2W wanting to trade forex need to know. This, combined with the stats you've posted thus far offer compelling evidence about risk management, leverage and choice of instrument.

Thanks Tim, I'm glad if the info I provided can be helpful to the OP and others.

On a separate note, I think I see what Purple Brain is driving at. I may have misunderstood him, but I think the general gist is along the lines of: did the traders who were profitable over the 3 month study period just get lucky and then crash 'n burn soon after, or were they able to repeat their success, indicating that they can take profits on a consistent basis over an extended period of time? I.e., did they just get lucky like the masses of long only equity traders in the run up to the dot com bubble in 2000, or have they acquired genuine lasting skill that enables them to trade in all types of markets - trending, range bound or otherwise!
Cheers,
Tim.

PB asked some great questions, and I definitely see the value in gathering data for longer time frames to see which traders continued to have success. While 6-month data wasn't covered in the original DailyFX studies, I have some more humble theories :cheesy: regarding your questions. Since, the percentage of profitable traders has remained fairly similar quarter after quarter for several years, I'm inclined to think this is not a case of traders doing well only in certain market conditions like what happened with the dot com bubble.

However, the question remains of how many of the traders who were profitable over 3 months continued to be profitable after 6 months or a year. This is something that we are currently studying with TopTradr. We're co-hosting a trading contest with this prop trading firm that wants to find people capable of producing consistent returns, so that firm can back these traders with their money. The reason FXCM got interested in the idea is because we used to host a monthly King of the Micro trading contest a few years ago, but found that the winners were seldom able to repeat their success. Only a handful of traders won the KOM contest multiple times. We hope that the new TopTradr format will highlight traders who achieve long term success and impart their knowledge to others.

 

[Purple Brain]

Timsk - I’m glad someone else got what I was getting at.

Jason - I’m going to assume it is my fault in lacking the necessary articulation, erudition and intelligence to pose the question in such a way that you could provide a clear answer.

However, others viewing this thread may not be quite so charitable in their assessment of your responses.

Forget 3 months, 6 months – you’re getting hung up on something that isn’t the central issue.

I’ll give it one more try.

Archie, Bertie, Charlie, Dave, Edward, Frank, Gordon, Harry, Ian and James all place their first trade with FXCM on the same day. After 12 months how many of those original 10 are still actively trading AND have an account showing profits from their trading activities.

There is churn in every brokerage. Clients come client go. But there remain a small core of clients who are successful. For every 100 clients that come on board, many (most) will close their account or simply become dormant with less than they deposited within 12 months. What is that percentage?

FXCM has that data. Every broker has that data. They are the only ones who know the reality of trader success/failure. Would you be prepared to share that data with us?

 

[Purple Brain]

Had a brainwave. Forget everything that’s gone before regarding my query.

Regardless of whether an account is closed, dormant, active – of all the client accounts FXCM has and has had - all of them - what percentage of these meet the following criteria:-

(Withdrawals + Current Balance) > (Deposits).

Thanks.

 

[Rhody Trader]

Do you have access to any data which would shed light on the query I made on trader longevity Rhody Trader?

I think a blog post I did earlier in the year speaks to your question: Starting to detail forex profitability data, which generated a bit of thread conversation here.

 

[Purple Brain]

I think a blog post I did earlier in the year speaks to your question: Starting to detail forex profitability data, which generated a bit of thread conversation here.

Many thanks Rhody Trader. Nothing beats an intelligent analysis of empirical data.

“In other words, the consistency rate is low in general terms. On average, less than half of those who make a profit in one quarter do so again in the next quarter. That means we can expect less than 15% of accounts profitable in one quarter to be so again the next, based on the broker-reported data. And seeing as the data I’m using here is from what looks to be a somewhat above average group of traders, we can probably shave a bit off even that 15%.
Furthermore, even among the 15% who are able to repeat, less than half are able to do it multiple times. That means not only is there no consistency among the profitable traders broadly, but there’s not a great deal among those who experience success – at least until you get further out into those who have a history of repeating.”.

Based on your analysis which I quote above, would it be reasonable to suggest from any given sample size of traders, by the end of the first 12 months trading, less than 2% will be generating consistent profits?

 

[Joules MM1]

2012 insight ....proviso: as reported

...the only ones who know the reality of trader success/failure. Would you be prepared to share that data with us?

 

[Purple Brain]

Jason (FXCM) - just occurred to me you may have thought I had the daggers out for you with my insistent questioning. Massive apologies if I gave that impression. I am in your debt for the excellent posts and data you have posted in this thread. It’s just that you are one of the few guys in a position to know the real answer to the question on trader mortality and put this mythical “95% lose” to bed once and for all. When I see an opportunity to extract information I tend to press it. One of my many character flaws.

I have absolutely no axe to grind with brokerages and realise they have a business model based on profitability for the organisation while providing – generally quite decent – facilities for their clients.

 

[Purple Brain]

2012 insight ....proviso: as reported

Your emphasis duly noted. LOL

 

[Rhody Trader]

Based on your analysis which I quote above, would it be reasonable to suggest from any given sample size of traders, by the end of the first 12 months trading, less than 2% will be generating consistent profits?

If we were to extrapolate from the observed persistence in the quarterly figures to say that only 50% of those who were profitable in one quarter were also profitable in the next, it would look at something like this:

30% profitable in Q1 (rough average of the quarterly figures for all brokers)
15% also profitable in Q2
7.5% also profitable in Q3
3.75% also profitable in Q4

I haven't looked at the numbers in a while and don't have them in front of me so I can't say how well that may be indicative of reality. I don't think it's too far off, though.

 

[timsk]

I haven't looked at the numbers in a while and don't have them in front of me so I can't say how well that may be indicative of reality. I don't think it's too far off, though.

Hi John,
If you plotted this on a chart it would be a straight descending line which, in effect, hits zero eventually. So, either all traders blow up eventually, or the line flattens out at some point to allow the elite handful to make consistent gains indefinitely. If it doesn't flatten out, then this would support the theory promulgated by some former members that traders simply get lucky and mistake their good fortune for real skill. The more their luck continues (i.e. Q4 taders and beyond), the more inclined they are to believe that's it's their trading skill that accounts for their success. Ultimately though, they're doomed to fail.

This begs the obvious question: at what point can a trader feel confident in their ability and know that they have a strategy with a positive expectancy that is sustainable in the long term? In other words, at what point can simple basic luck be ruled out as an explanation for their continued success?
Tim.

 

[Splitlink]

In other words, at what point can simple basic luck be ruled out as an explanation for their continued success?
Tim.

I do not think that luck can be ruled out of anything, even where or how we were born---least of all, trading. But one has to make an effort to get lucky, all through life, so buying shares when the market is dropping like lead, may produce some instant fortunes but it is not a thing that I would do, or recommend. Trading short term is very random, in my view. although I do it.

 

[neil]

I do not think that luck can be ruled out of anything, even where or how we were born---least of all, trading. But one has to make an effort to get lucky, all through life, so buying shares when the market is dropping like lead, may produce some instant fortunes but it is not a thing that I would do, or recommend. Trading short term is very random, in my view. although I do it.

Think of that little sperm travelling in space and grows into Price Charles - that's luck.

 

[Rhody Trader]

This begs the obvious question: at what point can a trader feel confident in their ability and know that they have a strategy with a positive expectancy that is sustainable in the long term? In other words, at what point can simple basic luck be ruled out as an explanation for their continued success?
Tim.

Tim, the last set of figures in my post at least moves us in that direction:

Among the 214 testable accounts with 4+ winning quarters, 171 (80%) were successful in going back-to-back more than half the time, with 67 being 100% successful (31%).

So if you can be profitable over 4 or more quarters you've got a good chance at sustaining success.

 

[Jason Rogers]

Jason (FXCM) - just occurred to me you may have thought I had the daggers out for you with my insistent questioning. Massive apologies if I gave that impression. I am in your debt for the excellent posts and data you have posted in this thread. It’s just that you are one of the few guys in a position to know the real answer to the question on trader mortality and put this mythical “95% lose” to bed once and for all. When I see an opportunity to extract information I tend to press it. One of my many character flaws.

I have absolutely no axe to grind with brokerages and realise they have a business model based on profitability for the organisation while providing – generally quite decent – facilities for their clients.

No offense taken, PB

If I could, I would provide you with more data on profitability stats, but I can only comment on what’s publicly available through DailyFX studies and FXCM’s quarterly reports to our regulators. The table Joules posted shows data from one of those quarterly reports last year.

What’s interesting is how even the data from other brokers seems to support the conclusions of the DailyFX studies on traders at FXCM, namely that accounts with higher balances tend to use less leverage and therefore perform better. That could explain why the two brokers with the highest profitability percentage happen to be the ones with highest account opening minimum ($10,000). However, this is only a partial picture, since we don’t know the average account size at all these brokers.

In the end, the biggest factor determining whether a trader is profitable or not is the strategy they use. A trader's results will be due to their own trading decisions on when to buy and sell. DailyFX research has found that retail traders often try to pick tops and bottoms, rather than trade with the trend. That is why the Speculative Sentiment Index (SSI), which I discuss extensively in our signals thread, can be used as a contrarian indicator.

When SSI is positive, that means retail traders are net long the currency pair, which is a bearish signal. On the other hand, a negative SSI means traders are shorting the pair overall, which is a bullish signal.

 

[barjon]

Hi John,
If you plotted this on a chart it would be a straight descending line which, in effect, hits zero eventually. So, either all traders blow up eventually, or the line flattens out at some point to allow the elite handful to make consistent gains indefinitely. If it doesn't flatten out, then this would support the theory promulgated by some former members that traders simply get lucky and mistake their good fortune for real skill. The more their luck continues (i.e. Q4 taders and beyond), the more inclined they are to believe that's it's their trading skill that accounts for their success. Ultimately though, they're doomed to fail.

This begs the obvious question: at what point can a trader feel confident in their ability and know that they have a strategy with a positive expectancy that is sustainable in the long term? In other words, at what point can simple basic luck be ruled out as an explanation for their continued success?
Tim.

That's not necessarily so, Tim. A trader may drop out of the figures because he has a losing quarter (who hasn't ) only to get back on his merry way the next quarter. Anyway what good is "positive expectancy" - that's all very nice but I guess someone doing for their only source of income is more worried about whether they are making enough to put bread on the table rather than just finishing up with a + sign every quarter.

As for luck, well that's something of a red herring in my view since you can define it in so many ways. For example, if people who have consistent, but short term, success have worked out a strategy that happens to suit the prevailing market conditions is that "lucky" - by one way of looking at it, yes. By another, no.

 

[Babyblush]

Traders fail because they are not intellectual enough while trading in the forex market and are entrapped with the wrong trades because of their emotions.

 

[VielGeld]

@Rhody: Would that perhaps be the wrong way to account for consistency? It's certainly one way of measuring it, but it has to be extremely tough to keep it up. We can't all have winning quarters, after all. Maybe measuring an average profitability over say 5 years would lend to a different view of profitability?

At the same time, I'm sure all the really good traders aren't retail. They have their own funds or work in institutions/companies that provide the kind of resources you wouldn't have access to as a retail. So the implication is that if someone is good enough as a retail guy, then he's going to move on up and the retail stats will suffer as a result.

But that said, some really good info has been posted for once. Thanks for that, Jason (despite *cough* promoting a few institutions, but I suppose I can overlook it for once).

 

[Purple Brain]

No offense taken, PB

Delighted to hear that.

If I could, I would provide you with more data on profitability stats, but I can only comment on what’s publicly available

I quite understand your predicament. But as I suggested to another member yesterday, even if every broker were required by law to state “98% of you will lose some or all of your money” it would have little effect. I am almost certain the majority of the 98% would imagine themselves to be part of the elite 2%. I know I do, in spite of significant empirical evidence to the contrary.

What’s interesting is how even the data from other brokers seems to support the conclusions of the DailyFX studies on traders at FXCM, namely that accounts with higher balances tend to use less leverage and therefore perform better. That could explain why the two brokers with the highest profitability percentage happen to be the ones with highest account opening minimum ($10,000).

That could also be an indication that those with more money are already successful traders or possibly even financial institutions who use brokers for hedging/arbing.

I thought I understood leverage/gearing and how that can hurt, but I’m not sure I do. I get 1:50 leverage on most FX pairs from OANDA, 1:20 on others. It wouldn’t matter if I got 1:100 or 1:1000, I’m still only going to risk the same fixed percentage of my trading capital on any one trade. Is it only if the individual trader uses leverage to risk more than a sensible fraction of their account on any one trade that leveraging is considered the culprit rather the traders stupidity?