Sharpen Calculation Skills

[Phylo]

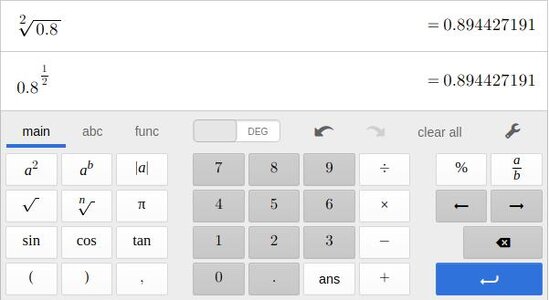
Good Joke (for mathematically inclined) – the nonsense should be fairly obvious. However, I wonder how obvious....

There is nothing special about today, this year, any other year or every 1,000 years.

1. If the age of anyone on the 31 December (note: the last day of the year) is added to the year of their birth the sum will – always = the current year, exact.
2. If the age of anyone is calculated before their birthday of the current year then the sum of their age + year of birth will – always = the current year - 1 year (the current year less 1 year).

Example 1:
Anthony Hopkins (an actor, by way of example - see wikipedea, if interested) was born 31 Dec 1937.

This year, at current date - 6 Dec 2022 - Anthony is 84 years old.
84 + 1937 = 2021.
This year, on 31 Dec 2022 - Anthony will be 85.
85 + 1937 = 2022. (the current year, exact)

Example 2:
Next year, on 1 Jan 2023 Anthony will - still - be 85.
85 + 1937 = 2022.
Next year, on the 31 Dec 2023 Anthony will be 86.
86 + 1937 = 2023. (the current year, exact)

LAUGH OF THE DAY – anyone interested in more calculations with basic calculus ?
Some may find of interest and swing traders may be inspired to rediscover mathematical entertainment and sharpening of calculation skills while waiting for swing alert/s.

To code more complex indicators and automations an understanding of at least basic Mathematics is, at times, required.

Calculating the FTSE 100

Came across this actual problem in a book I chanced to glance through. The book provides answers to questions. I provide solution calculations (accommodate any typos) - some basic calculus.

[Question - 5.2 Contextual Q:3]

• On a particular day, the Financial Times 100 Share Index (FTSE 100) opens in London at 4,000.
• During the rest of the day, its value t hours at 9 a.m. is given as F = 4,000 - 16t^2 + 8t^3 - 3/4t^4.
• A broker is instructed to sell* the client’s position only if the value of the FTSE is falling.
• * according to pre-agreed increments and criteria – not relevant to Question and Answers and solutions.

Comment: 16t^2 = 16 x (t to exponent 2) ; 8t^3 = 8 x (t to exponent 3) ; etc.

Questions:

1. What is the value of the FTSE at noon.
2. Calculate the highest value of the index during the day and at what time to the nearest minute did this occur.
3. If trading finishes at 4.30 p.m., by how much has the index risen or fallen during the day.
4. During which times of the day could the broker have sold off the clients position ?

Answers:

1. 4011.3 points. note: indexes are designated in points (professionally) not pips.
2. 4183.9 points at 3.19 p.m.
3. Rise of 102.0 points at 4.30 p.m.
4. Between 9 a.m. and 10.41 a.m. and between 3.19 p.m. and 4.30 p.m.

SOLUTIONS:

Solution A:
12.00 (noon) - 9.00 = 3. Therefore: t = 3. Note: 9.00 a.m. ~ t = 0; 10 a.m ~ t = 1; 11.00 a.m ~ t =2; 12.00 p.m. ~ t = 3.

At 9.00 a.m ~ t = 0
F = 4,000 - 16t^2 + 8t^3 - 3/4t^4
F= 4,000 - 16(0^2) + 8(0^3) - 3/4(0^4)
F= 4,000 - 16(0) + 8(0) - 3/4(0)
F= 4,000 - 0 + 0 - 0
The index = 4,000 points at 9.00 a.m. or when time t = 0.

At 12.00 ~ t = 3
F = 4,000 - 16t^2 + 8t^3 - 3/4t^4
F= 4,000 - 16(3^2) + 8(3^3) - 0.75(3^4)
F = 4,000 - 16(9) + 8(27) - 0.75(81)
F = 4,000 - 144 + 216 - 60.75
F= 4,011.25
F= 4,011.3

Answer A: The index vaue is 4,011.3 points at noon (12.00 p.m.)

Solution B:
See YouTube for basic differentiation

• Differentiate F(t) to determine local and absolute maximum/minimum values.

On a graph t(time) would be the horizontal axis and F (points) would be the vertical axis.
Normally the horizontal axis is designated the x-axis with x-values and the vertical axis is designated y-axis with y-values.
In this instance t(time) is equivalent to the x-axis and index point values equivalent to the y-axis. ---> this may help:

F = 4,000 - 16t^2 + 8t^3 - 3/4t^4
F'(t) - differentiated = -32t + 24t^2 -3t^3
Note: F'(t) is differentiated to the first order; F"(t) is defferentiated to the second order.
F"(t) = -32 + 48t - 9t^2
F'"(t) = 48 -18t

Note:
F = 4,000 - 16t^2 + 8t^3 - 3/4t^4 can also be arranged as - pay attention to (-) signs and (+) signs -
F = -3/4t^4 + 8t^3 - 16t^2 + 4,000.
F'(t) = -32t + 24t^2 -3t^3 can also be arrange as
F'(t) = -3t^3 + 24t^2 - 32t.
The latter is the normal way - presenting expressions/equations in decending exponential order of power - but it is not necessary.
It also become tedious to be pedantic about exact/strict/rigorous mathematical notation when knocking off a few quick solutions.
However, whether decending or assending, incremental exponential order of powers should be maintained.

Factorise - t:
-32t + 24t^2 -3t^3 = t(-32 + 24t - 3t^2)
a: t=0,
b: -32+24t-3t^2 = 0 or rearranged b: -3t^2+24t-32 (see above Note)

Apply -
quadratic formula to -32 + 24t - 3t^2 or
cubic formula to -32t + 24t^2 -3t^3

Sharp EL-W505T, may be suitable, cheap and considered superior features to comparable Casio – and bonus one key press ease of access re Pi - (not referal links) https://www.amazon.co.uk/Sharp-EL-W5.../dp/B07PHT9LN4 / https://www.sciencestudio.co.uk/product/sharp-el-w506t/

Applying quadratic formular to -32 + 24t - 3t^2
(note: calculator inputs will be in order, -3,+24,-32)
Then:
t2 = 1.690 (derived from factorisation -> quadratic formular calculation) [calculator or pen/paper if hardcore]
t3 = 6.309 (derived from factorisation -> quadratic formular calculation)
and t1 = 0 (derived from factorisation - refer a: )

Applying qubic formular to -32t + 24t^2 - 3t^3 (note: calculator inputs will be in order, -3,+24,-32,0)
Then:
t1 = 0 (derived from cubic formula calculation) [calculator or pen/paper if hardcore]. Note: The 'solve any cubic-synthetic division method' as touted by clickbate YouTuber's is not univeral and only solve for the YouTuber's cherry-picked equations. For a fuller understanding of cubic formular see - Enhancements - at end of post
t2 = 1.690 (derived from cubic formula calculation)
t3 = 6.309 (derived from cubic formula calculation)

Process t1
F1 = 4,000 - 16t1^2 + 8t1^3 - 3/4t1^4
F1 = 4,000 - 16(0^2) + 8(0^3) - 4/4(0^4)
F1 = 4,000 - 0 + 0 - 0
F1 = 4,000 (point value at t = 0 or 9.00 a.m.)

Process t2
F2 = 4,000 - 16t2^2 + 8t2^3 - 3/4t2^4
F2 = 4,000 - 16(1.69^2) + 8(1.69^3) -3/4(1.69^4)
F2 = 4,000 - 16(2.8561) + 8(4.826809) - 0.75 (8.15730721)
F2 = 4,000 - 45.6976 + 38.614472 -6.117980408
F2 = 3,986.798892
F2 = 3,986.8 points
Calculating time: 1.69
Minutes: .69(60) = 41.4 = 41
Hours: 9.00 + 1 = 10
Time2 = 10.41

Process t3
F3 = 4,000 - 16t3^2 + 8t3^3 - 3/4t3^4
F3= 4,000 - 16(6.309^2) + 8(6.309^3) -3/4(6.309^4)
F3= 4,000 = 16(39.8034) + 8(251.120) - 0.75(1,584.317)
F3 = 4,000 - 636.855 + 2,008.96 - 1,188.237
F3 = 4,183.868
F3 = 4,183.9
Calculation time: t = 6.309.
Hours: 9:00 + 6 = 15
Minutes: .309(60) = 18.54 = 19
Time3 = 15:19 = 3.19 p.m.

Answer B: The highest value of the index is 4,183.9 points at 3.19 p.m.

Solution C:
Time: t = 16.30 - 9.00 = 7.30 ; 30 minutes / 60 minutes = 0.5 ; t = 7.5
F = 4,000 - 16t^2 + 8t^3 - 3/4t^4
F = 4,000 - 16(7.5^2) + 8(7.5^3) - 0.75(7.5^4)
F= 4,000 - 16(56.25) + 8(421.875) - 0.75(3,164.0625)
F= 4,000 - 900 + 3375 - 2373.146875
F = 4,101.853125
F = 4,102
4,102 - 4,000 = 102

Answer C: The index has risen by 102 points at 4.30 p.m.

Solution D:
At 9.00 a.m. point value = 4,000.0
At 10:41 a.m. point value = 3,986.8 (this was the min value- determined by 1st level calculus differentiation)
At 3.19 p.m. point value = 4,183.9 (this was the max value-determined by 1st level calculus defferentiation)
At 4.30 p.m point value = 4,102.0
The index was falling between 9.00 a.m and 10.41 a.m. and 3.19 p.m. and 4.30 p.m.

Answer D: The broker could have incrementally sold off the client's position between 9.00 a.m - 10.41 a.m and 3.19 p.m. and 4.30 p.m.

Additional Material:

• Scientific Calulator, Online Graphing Calculator - www.desmos.com/calculator , pen + paper required.
• Refresher Kit (1 of 2/3) http://www.pdfdrive.com/complete-pur...184782396.html (sign in not required).

Enhancements

Note: Solve 'any' Cubic Equations - Synthetic Division Method: as touted by clickbate-youtubers is not a universal solution method as made to believe and will eventually fail outside the scope of clickbate-youtuber example criteria.

Mathologer is solid-bonafide-professional.

 

[Phylo]

Margin Calculations

This post is copy & paste with minor rearrangements of my FF post 27-Apr-2016.

1 micro lot = 0.01 = 1,000 currency units.
1 mini lot = 0.10 = 10 micro lots = 10,000 currency units.
1 lot = 1.0 = 10 mini lots = 100 micro lots = 100,000 currency units.

The first currency of a forex pair is the base currency and the second is the quote currency.
Easy remembrance: Alphabetically b is before q → (b) base first / (q) quote second.
Example: GBP/USD = base/quote

The below gives a sense of the scope of available margin ratios and the differences between deposit currency and base currency at parity and deposit currency and base currency subject to exchange rates.

Weekday and Weekend Margins Dukascopy Bank: https://www.dukascopy.com/europe/eng...counts/margin/

Account Deposit Currency: GBP
Currency Pair: GBP/USD
Position Size: 1 lot (100,000 currency units)
Margin Rate: deposit currency / base Currency = 1 GBP / 1 GBP = 1

margin = margin rate x exchange rate x position size in currency units. *

* exchange rate = account deposit currency/base currency

If the account deposit currency is the same as the base currency the exchange rate will be parity (1).

• 1:30 margin = 1/30 x 1 x 100,000 = 3,333 GBP.
• 1:60 margin = 1/60 x 1 x 100,000 = 1,667 GBP.
• 1:90 margin = 1/90 x 1 x 100,000 = 1,111 GBP.
• 1:100 margin = 1/100 x 1 x 100,000 = 1,000 GBP.
• 1:200 margin = 1/200 x 1 x 100,000 = 500 GBP.
• 1:300 margin = 1/300 x 1 x 100,000 = 333 GBP.

Account Deposit Currency: USD
Currency Pair: GBP/USD
Position Size = 1 lot (100,000 currency units)
Exchange Rate: deposit currency / base currency = 1.499 USD / 1 GBP

• 1:100 margin = 1/100 x 1.459/1 x 100,000 = 1,459 USD
• 1:30 margin = 1/30 x 1.459/1 x 100,000 = 4,863 USD.

Account Deposit Currency: GBP
Currency Pair: EUR/JPY
Position Size: 1 lot (100,000 currency units)
Exchange Rate: deposit currency / base Currency = 1 GBP / 1.29 EUR

• 1:100 margin = 1/100 x 1/1.29 x 100,000 = 775 GBP
• 1:30 margin = 1/30 x 1/1.29 x 100,000 = 2,583 GBP

Account Deposit Currency: USD
Currency Pair: EUR/JPY
Position Size: 1 lot (100,000 currency units)
Exchange Rate: deposit currency / base currency = 1.13 USD / 1 EUR

• 1:100 margin = 1/100 x 1.131/1 x 100,000 = 1,131 USD
• 1:30 margin = 1/30 x 1.131/1 x 100,000 = 3,770 USD

Note: Some brokers have fixed margins and pairs where the deposit currency and the base currency are not at parity and would otherwise be subject to exchange variation are given an added currency padding and the margin locked at a set value.

Note: If the Dukascopy link is accessed it will be noted that while Dukascopy designates FX units like for like (1,000 units as 1,000 units) lots are designated as follows: 0.01 lot as 0.001 million, 0.1 lot as 0.01 million and 1.0 lot as 0.1 million (100,000/1,000,000 = 0.1).

 

[Phylo]

pi

 

[Phylo]

3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679xxxxxxxxxxxxxxxxxx...........................................................................

 

[Phylo]

Part 1 - How to multiply using lines | Japanese multiplication | Zero math

Part 2 - How to multiply using lines | Japanese multiplication | Zero math

 

[Phylo]

The Korean king's magic square: a brilliant algorithm in a k-drama (plus geomagic squares)

 

[BigDeal]

How to multiply using lines | Japanese multiplication | Zero math

Genius !

 

[Phylo]

Easy Percentage Calculation
When either required percentage or base number ends in zero.

1: 20% of 30
Long: (20 x 30)/100 = 6
Short - easy: 20/10 x 30/10
(dividing each number by 10 = shift decimal pint 1 place left.
2 x 3 = 6

2: 30% of 80
Long: (30 x 80)/100 = 24
Short - easy: 30/10 x 80/10
3 x 8 = 24

3: 20% of 60.6
2 x 6.06 = 12.12

4: 25% of 80
2.5 x 8 = 20

5: 2.5% of 40
0.25 x 4 = 1

6: 0.35% of 70
0.035 x 7 = 0.245

7: 20% of 160
2 x 16 = 32

 

[Phylo]

Depreciation of Assets : Part 1

Assets like vehicles normally depreciate over time and other assets like property normally appreciate over time.

These calculations should be modelled in a spreadsheet for ease of convenience and permanent record access. Free online spreadsheets are available through the well known sources. Modelling spreadsheet formulas for these calculations is beyond the scope of this brief.

There are a number of depreciation models. This brief deals with simple constant depreciation. Assets can run into thousands and millions of £, $, € or other currencies. In order to avoid unwieldy large numbers which can add to confusion, a value of £10.00 will be used - the value of a genuine Rolex* bought from the local junkie on the corner of Crack and Pipe street.

* can't think of a more useless asset to dangle on one's person - however, I am not into the watch business.

1. Asset value: £10
2. Asset depreciation: 20% per year. Note: 20% = 20/100 = 0.2
3. * = multiply
3. x = unknown (not multiply), x is normally used as unknown variable in maths. Any letter (a, g, d etc) can be used but I will stick with the most used notation.

For clarity assume the Rolex bought on 1 Jan 2000 and the value of the Rolex is £10.

1st year depreciation = 10.00 * 0.2 = 2.00.
10.00 - 2.00 = £8.00
On 1 Jan 2001 the value of the Rolex is £8.00

2nd year depreciation = 8.00 * 0.2 = 1.60.
8.00 - 1.60 = £6.40.
On 1 Jan 2002 the value of the Rolex is £6.4

The second step 10.00 - 2.00 = £8.00 and 8.00 - 1.6 0 = £6.40 can be eliminated.

Note: If an asset is reduced by 20% its value will be 80% (100%-20% = 80%). Note: 80% = 80/100 = 0.8. (or 1.00 - 0.2 = 0.8)

0 year value after depreciation = £10.00
1st year value after depreciation = 10.00 * 0.8 = £8.00.
2nd year value after depreciation 8.00 * 0.8 = £6.40
3rd year value after depreciation 6.40 * 0.8 = £5.12
4th year value after depreciation 5.12 * 0.8 = £4.096
5th year value after depreciation 4.096 * 0.8 = £3.2768 (#) see below

If 10 is punched into a calculator and multiplied by .8 it will return 8, now if 8 is multiplied by .8 it will return 6.4 and 6.4 multiplied by .8 it will return 5.12 - you get the idea.

The above calculations can be thought of as
1st year: 10.00*0.8 = £8.00
2nd year: (10.00*0.8)*0.8 = £6.50
3rd year: ((10.00*0.8)*0.8)*0.8 = £5.12

A more efficient way to express the above is
1st year: 10.00*0.8 = £8.00
2nd year: 10.00*0.8^2 = £6.40 note: 0.8^2 = 0.8 to exponent 2
3rd year: 10.00*0.8^3 = £5.12

This way, we can shortcut straight to any relevant year by use of the exponent value corresponding to the year. i.e. 5th year, exponent value = 5.
4th year: 10.00*0.8^4 = £4.096
5th year: 10.00*0.8^5 = £3.2768 (so, as above (#) 5th year value after depreciation 4.096 * 0.8 = £3.2768)

Depreciation of Assets : Part 2

We know from the above that value after depreciation for the 1st year is £8.

The question arises, how to calculate - at the current 20% depreciation rate - the value of the Rolex after (A) 6 month and (B) for every financial quarter, aka every 3 months and (C) for every month of the year.

ANS A:
We know from 1st year calculation >> 10.00*0.8 = £8.00 which actually is 10.00*0.8^1 = £8.00 but we do not include the ^1 for ease of convenience as it is not necessary.

So £8.00 represents the Rolex value after 1 year of 20% depreciation.

Then: 12 months divide by 6 months = 2.

Let x = unknown value.

Then 10.00*x^2 = £8.00

Then x^2 = 8.00/10.00 (this and the following steps is usually termed manipulation or rearrangement of formula and YouTube is full of easy to understand instructions)

Then, x = root 2 of 8/10 (note: 8/10 = 0.8), so x = root 2 of 0.8 = 0.894427191
The above can also be expressed as 0.8^1/2 = 0.894427191

Demos - online Scientific Calculator : https://www.desmos.com/scientific

The result 0.894427191 can be stored in a calculator memory and recalled for calculation

So,
Value at end of 1st 6 months of year 1 = 10.00*0.894427191 = £8.94427191
Value at end of 2nd 6 months of year 1 = 10.00*0.894427191^2 = £8.00
Value at end of 1st 6 months of year 2 = 10.00*0.894427191^3 = £7.155417528
Value at end of 2nd 6 months of year 2 = 10.00*0.894427191^4 = £6.40
Alternatively
Value at end of 1st 6 months of year 1 = 10.00*0.8^1/2 = £8.94427191
Value at end of 2nd 6 months of year 1 = 10.00*0.8^2/2 = 10*0.8 = £8.00
Value at end of 1st 6 months of year 2 = 10.00*0.8^3/2 = £7.155417528
Value at end of 2nd 6 months of year 2 = 10.00*0.8^4/2 = 10.00*0.8^2 = £6.40

We can see value £8.00 and £6.40 tally with above for value at end of 1st and 2nd year.

ANS B:

The logic is the same as above.

So £8.00 represents the Rolex value after 1 year of 20% depreciation.

Then (B) every financial quarter is represented as 3 months and 12 months divide 3 month = 4.

Let x = unknown value.

Then 10.00*x^4 = £8.00

Then x^4 = 8.00/10.00

Then, x = root 4 of 8/10 (note: 8/10 = 0.8), so x = root 4 of 0.8 = 0.945741609
The above can also be expressed as 0.8^1/4 = 0.945741609

The result 0.945741609 can be stored in memory and recalled for calculation

So,
Value at end of 1st financial quarter - 1st 3 months of year 1 = 10.00*0.945741609 = £9.45741609
Value at end of 2nd financial quarter - 2nd 3 months of year 1 = 10.00*0.945741609^2 = £8.94427191
Value at end of 3rd financial quarter - 3rd 3 months of year 1 = 10.00*0.945741609^3 = £8.458970107
Value at end of 4th financial quarter - 4th 3 months of year 1 = 10.00*0.945741609^4 = £8.00

Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.945741609^5 = £7.565932872
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.945741609^6 = £7.155417528
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.945741609^7 = £6.767176086
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.945741609^8 = £6.40
Alternatively
Value at end of 1st financial quarter - 1st 3 months of year 1 = 10.00*0.8^1/4 = £9.45741609
Value at end of 2nd financial quarter - 2nd 3 months of year 1 = 10.00*0.8^2/4 = £8.94427191
Value at end of 3rd financial quarter - 3rd 3 months of year 1 = 10.00*0.8^3/4 = £8.458970107
Value at end of 4th financial quarter - 4th 3 months of year 1 = 10.00*0.8^4/4 = 10.00*0.8 = £8.00

Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^5/4 = £7.565932872
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.8^6/4 = £7.155417528
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.8^7/4 = £6.767176086
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.8^8/4 = 10.00*0.8^2 = £6.40

We can see that values, £8.94427191, £8.00, £7.155417528 and £6.40 tally with their respective above equivalents.

ANS C:
Would follow the same logic as ANS A & B.

 

[Phylo]

Depreciation of Assets : Part 3

With reference to the above

Value at end of 1st financial quarter - 1st 3 months of year 1 = 10.00*0.8^1/4 = £9.45741609
Value at end of 2nd financial quarter - 2nd 3 months of year 1 = 10.00*0.8^2/4 = £8.94427191
Value at end of 3rd financial quarter - 3rd 3 months of year 1 = 10.00*0.8^3/4 = £8.458970107
Value at end of 4th financial quarter - 4th 3 months of year 1 = 10.00*0.8^4/4 = 10.00*0.8 = £8.00

Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^5/4 = £7.565932872
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.8^6/4 = £7.155417528
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.8^7/4 = £6.767176086
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.8^8/4 = 10.00*0.8^2 = £6.40

The following can be expressed

Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^1+1/4 = £7.565932872
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.8^1+2/4 = £7.155417528
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.8^1+3/4 = £6.767176086
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.8^1+4/4 = 10.00*0.8^2 = £6.40

or

Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^1+0.25 = £7.565932872
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.8^1+0.5 = £7.155417528
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.8^1+0.75 = £6.767176086
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.8^1+1 = 10.00*0.8^2 = £6.40



The implication of the year 2 relevant exponential value as 1+x/x or 1+x.xx should be quite obvious.

• It can be deducted - year 1 relevant exponential value can be expressed as 0+x/x or 2+x.xx, thus x/x or x.xx.
• It can be deducted - year 2 relevant exponential value can be expressed as 1+x/x or 1+x.xx.
• It can be deducted - year 3 relevant exponential value can be expressed as 2+x/x or 2+x.xx.
• It can be deducted - year 4 relevant exponential value can be expressed as 3+x/x or 3+x.xx.
• etc.

 

[Phylo]

Depreciation of Assets : Part 4

While the above half year and quarterly calculations may be acceptable in most instances they are not precisely accurate due to the following -

• A non leap years has 365 days and a leap year has 366
• A non leap year 1st quarter has 90 days and a leap year 91 days.
• A non leap year and leap year 2nd quarter has 91 days.
• A non leap year and leap year 3rd quarter has 92 days.
• A non leap year and leap year 4th quarter has 92 days.
• A non leap year has 90 + 91 + 92 + 92 = 365 days.
• A leap year has 91 + 91 + 92 + 92 = 366 days.

For a non leap year

• 1st quarter = 90 days
• 1st + 2nd quarter = 90 + 91 = 181 days.
• 1st + 2nd + 3rd quarter = 90 + 91 + 92 = 273 days
• 1st + 2nd + 3rd + 4th quarter = 90 + 91 + 92 + 92 = 365 days

So..

Acceptable :
Value at end of 1st financial quarter - 1st 3 months of year 1 = 10.00*0.8^1/4 = £9.45741609
Value at end of 2nd financial quarter - 2nd 3 months of year 1 = 10.00*0.8^2/4 = £8.94427191
Value at end of 3rd financial quarter - 3rd 3 months of year 1 = 10.00*0.8^3/4 = £8.458970107
Value at end of 4th financial quarter - 4th 3 months of year 1 = 10.00*0.8^4/4 = 10.00*0.8 = £8.00

Precision : with respect to days - not minutes, seconds, milliseconds, microseconds or nanoseconds.
Value at end of 1st financial quarter - 1st 3 months of year 1 = 10.00*0.8^90/365 = £9.464646117
Value at end of 2nd financial quarter - 2nd 3 months of year 1 = 10.00*0.8^181/365 = £ 8.952477822
Value at end of 3rd financial quarter - 3rd 3 months of year 1 = 10.00*0.8^273/365 = £ 8.462849554
Value at end of 4th financial quarter - 4th 3 months of year 1 = 10.00*0.8^365/365 = 10.00*0.8 = £8.00

Of note:

• 1/4 = 0.25 and 90/365 = 0.2465...
• 2/4 = 0.50 and 181/365 = 0.4958....
• 3/4 = 0.75 and 273/365 = 0.7479.....
• 4/4 = 1 and 365/365 = 1

Acceptable :
Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^1+1/4 = £7.565932872
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.8^1+2/4 = £7.155417528
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.8^1+3/4 = £6.767176086
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.8^1+4/4 = 10.00*0.8^2 = £6.40

Precision :
Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^1+90/365 = £7.571716894
Value at end of 2nd financial quarter - 2nd 3 months of year 2 = 10.00*0.8^1+181/365 = £7.161982258
Value at end of 3rd financial quarter - 3rd 3 months of year 2 = 10.00*0.8^1+273/365 = £6.770279643
Value at end of 4th financial quarter - 4th 3 months of year 2 = 10.00*0.8^1+365/365 = 10.00*0.8^2 = £6.40



The following should be apparent

Acceptable :
Value at end of 1st month of year 2 = 10.00*0.8^1+1/12 = £7.852612239
Value at end of 2nd month of year 2 = 10.00*0.8^1+2/12 = £7.707939872
Value at end of 3rd month of year 2 = 10.00*0.8^1+3/12 = £7.565932872
Note - as above: Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^1+1/4 = £7.565932872

Precision :
Value at end of 1st month of year 2 = 10.00*0.8^1+31/365 = £7.849812323
Value at end of 2nd month of year 2 = 10.00*0.8^1+(31+28)/12 = 0.00*0.8^1+ 59/365 = £7.71658387
Value at end of 3rd month of year 2 = 10.00*0.8^1+(31+28+31)/12 = 10.00*0.8^1+90/365 = £7.571716894
Note - as above: Value at end of 1st financial quarter - 1st 3 months of year 2 = 10.00*0.8^1+90/365 = £7.571716894

Graph: Year 2 - Monthly depreciation against monthly days
New >> (0, 10) Label: New
Graph line is drawn and aligns with dots via formula: y = 10.00*0.8^1+x/12 (last entry bottom left)