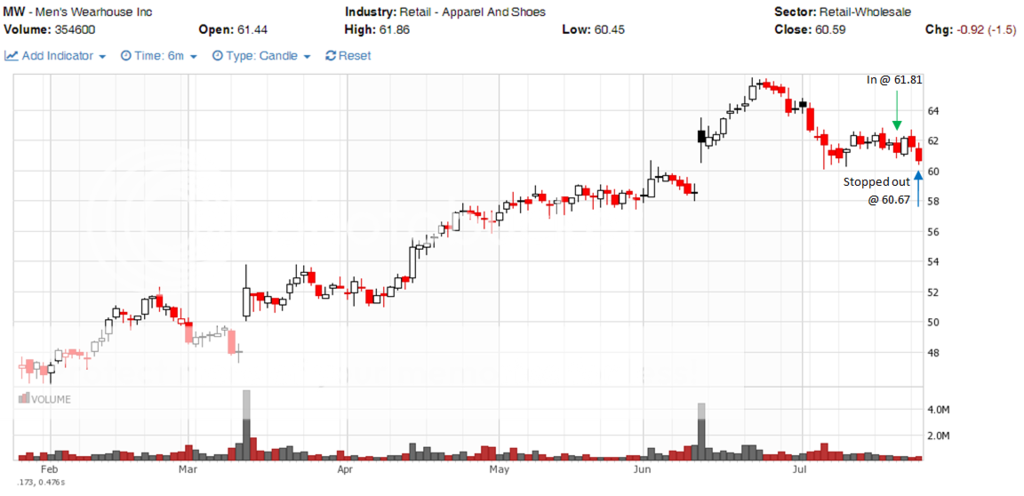
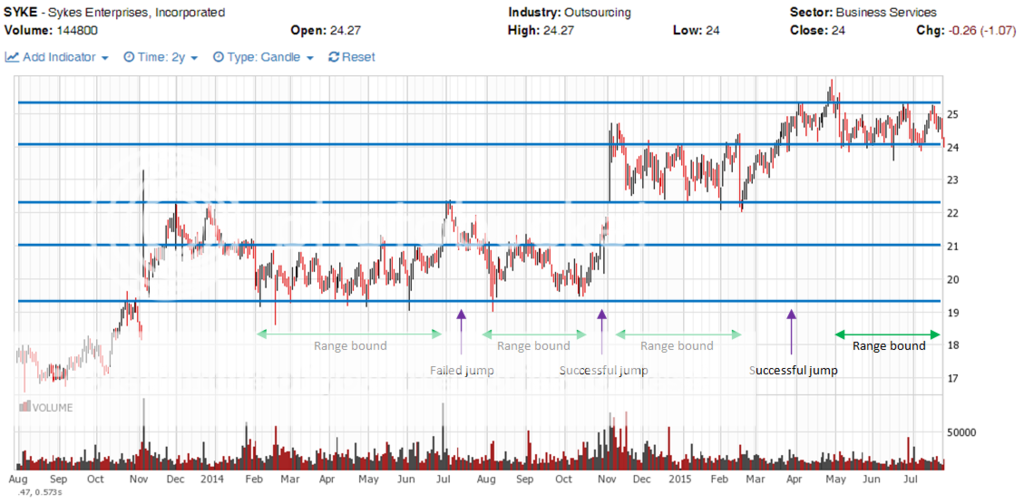
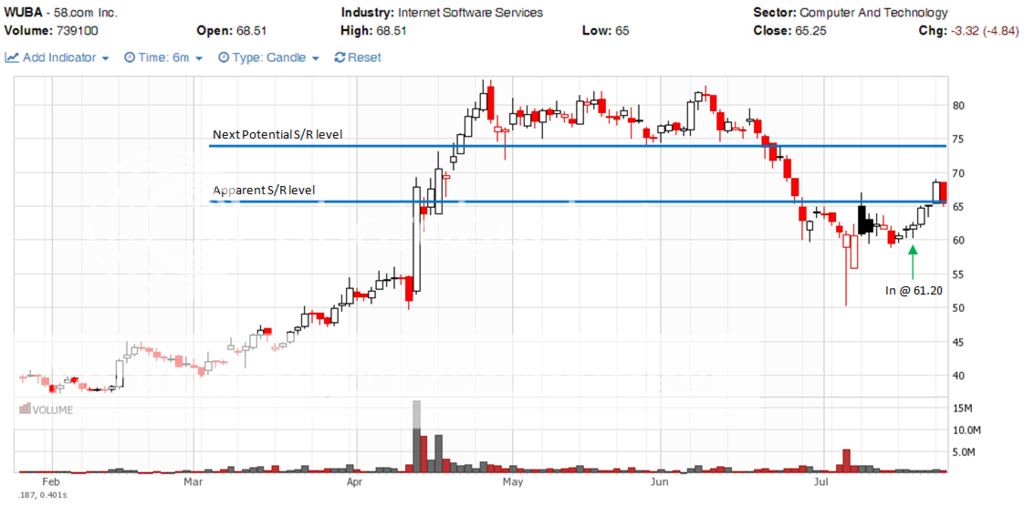
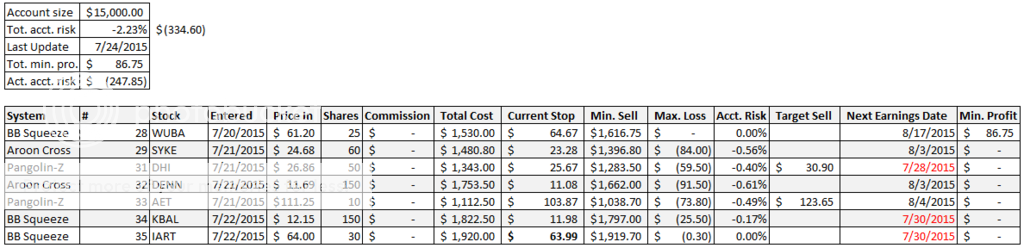
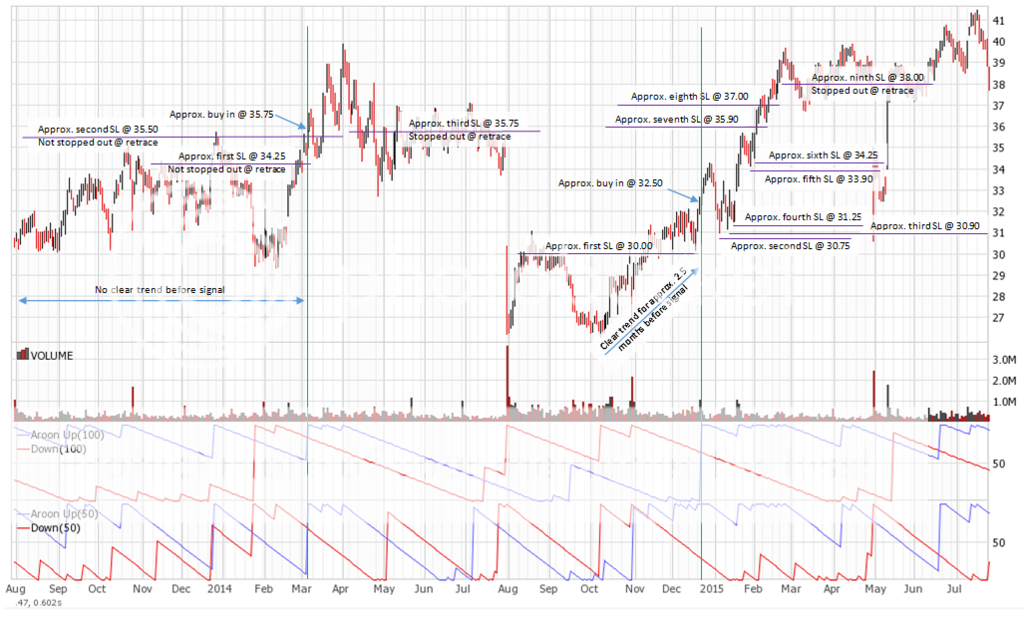
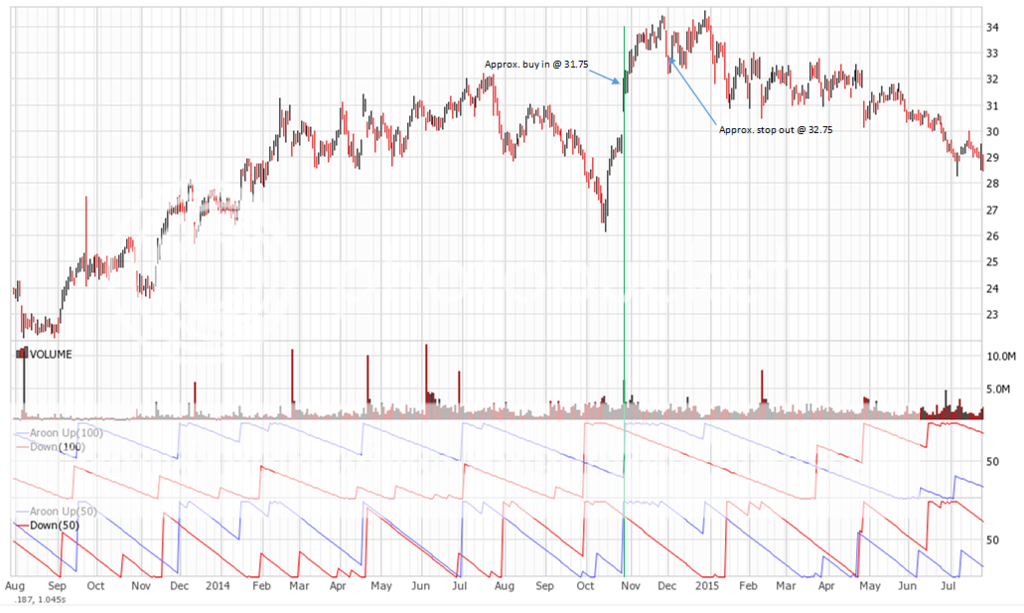
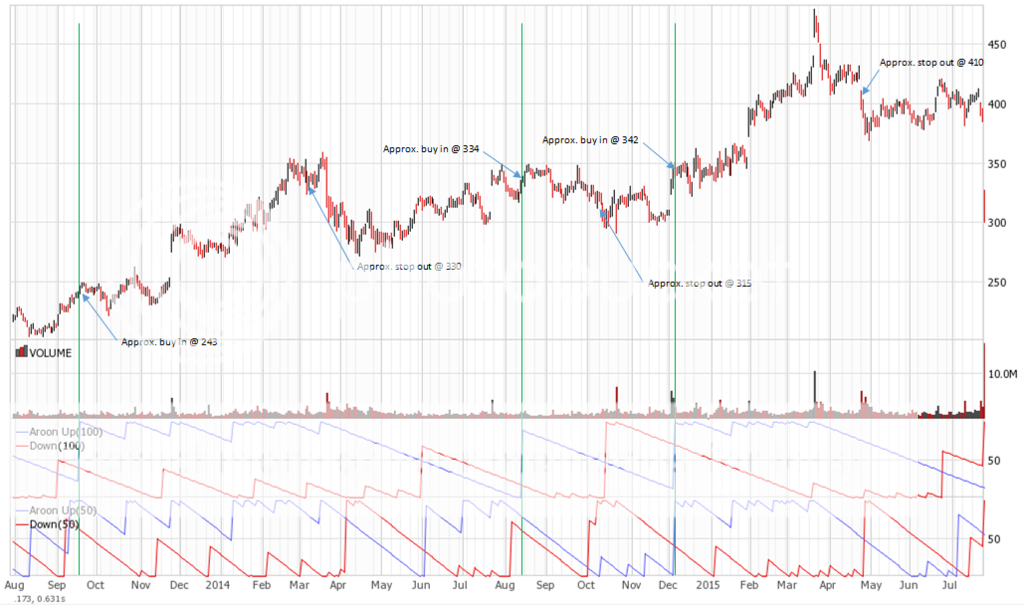
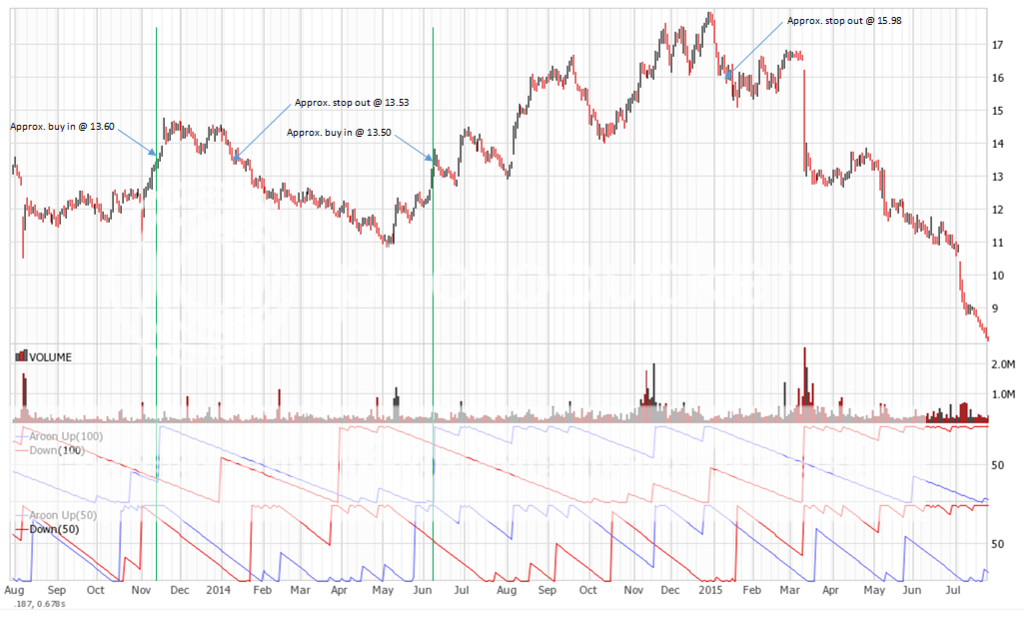
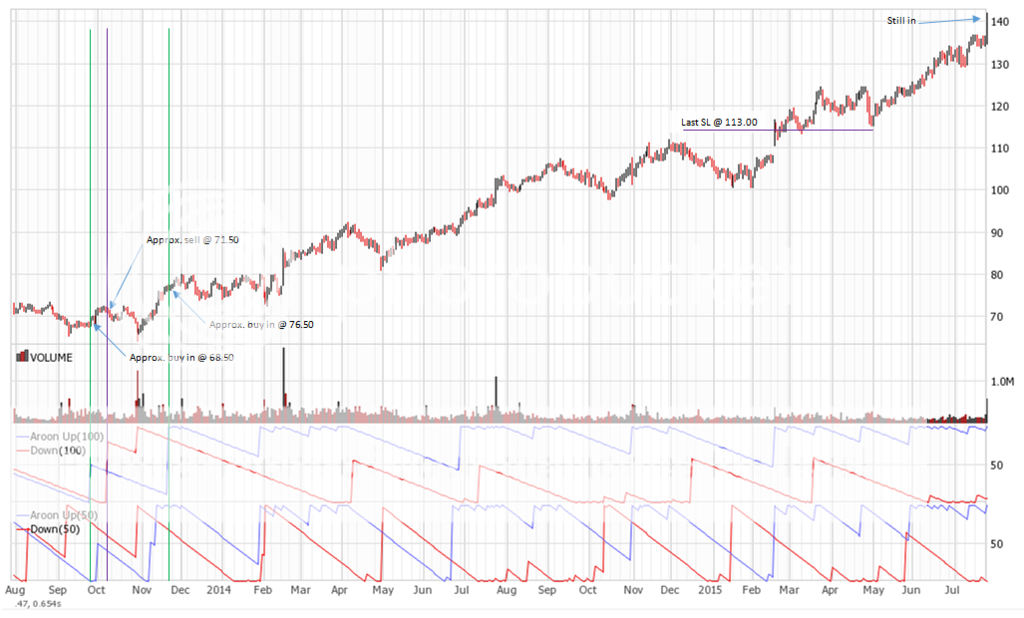
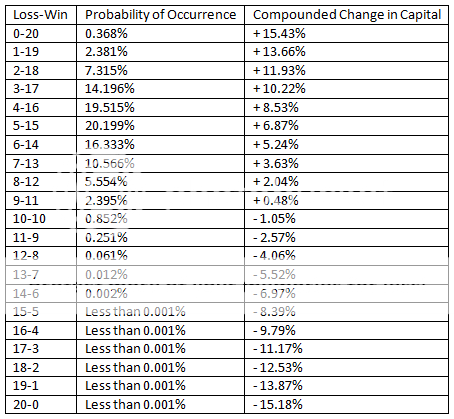
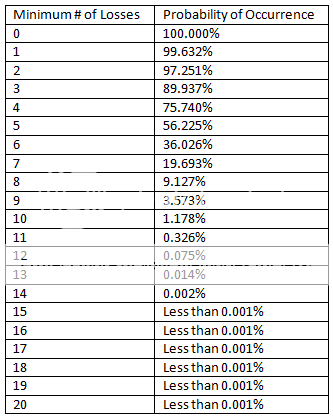
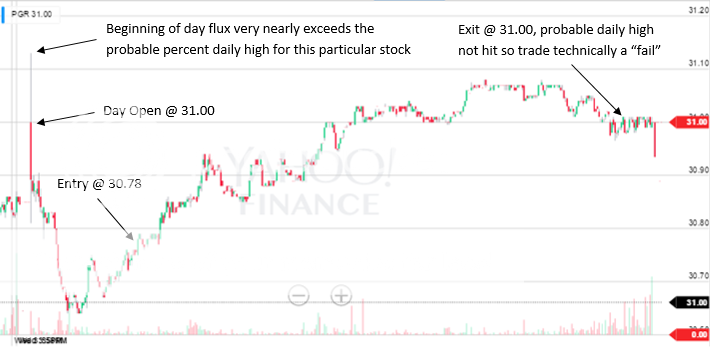
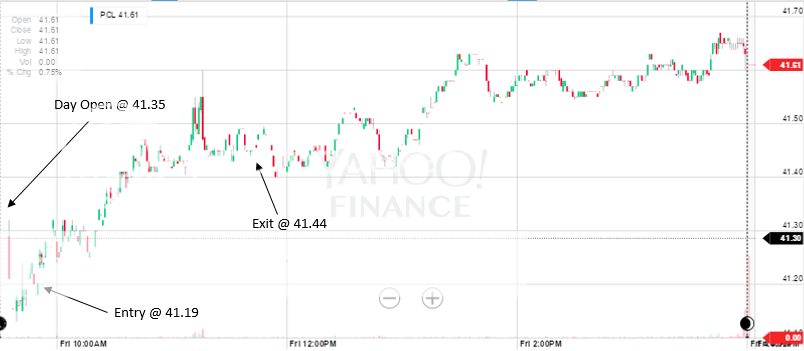
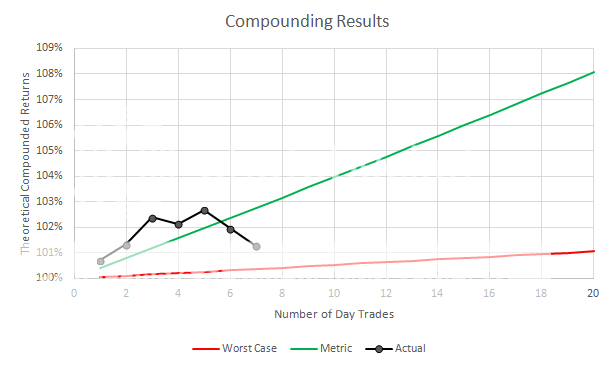
Join me on my journey to either bankruptcy or financial freedom. I have begun this journey after coming to some realizations:
1. I do not want to spend my life working. I do not need a huge stack of cash to enjoy life, and would rather spend my time on hobbies where I am my own boss than at a high paying job.
2. I can manage my cash as well as “professional” brokers. The catalyst that began my journey was after watching my “professionally managed” $45,000 investment account at Charles Schwab continuously decline to a meager $3,000 between 2011 and 2015. I figured I can do at least that good, so I moved my funds over to an account I now manage and have started trading myself.
After a month of trading with no real plan and getting a feel for how it works, I realized that I can’t just wing it and do well. I have developed a few trading plans that I am now testing out and sticking to rigidly. Over time I may add more plans, evolve my current ones, etc., but there will always be a plan for the trade I am executing and it will be formed prior to executing it and it will be stuck to.
In order to achieve my ultimate goal of becoming financially independent, I am setting some smaller goals:
1. Cut my current monthly spending by a third. This should be easily doable by cooking more. By doing this I will be able to add approximately half my monthly paycheck into my trading account.
2. Lose no more than 5% of the starting value of my account in any month. In order to help achieve this I will:
a. Not risk any more than 1.5% and rarely any more than 1% of my account on any trade. While live testing new strategies, I will not risk more than half of this.
b. Follow my execution plans and wait for appropriate times to enter into trades. No trading just to be trading.
c. Not have any more than 5% of my starting account balance for each month at risk at any point in time. If a trade moves so my stop loss puts me above my entry, the trades risk drops to 0 and I can enter new positions.
d. Not add more than 3% of risk to my starting account balance for each month on any single day. This should limit my new positions for each day to approximately 2-4.
I will declare myself financially independent once one of the following occurs:
1. The average income I generate from trading exceeds my job income over a 6 month period.
2. The size of my trading account exceeds my typical monthly expenses by 100% and I have had 4 consecutive 3 month periods with gains averaging greater than 5% of my starting account balance that month and no losing 3 month period in this timeframe.
3. The size of my trading account exceeds my typical monthly expenses by 200%.
I will stop trading and accept that my life fate is to work like most people once one of the following occurs:
1. I have a 12 month period with a net loss on all closed trades.
2. I have 4 consecutive months of losing more than 5% of the starting value of my account that month.
3. I have a 3 month period with a net loss that is a direct result of violating the trading rules and systems I have set in place.
I have determined that a handful of long term and a larger number of short term trades will be the best and most practical way for me to achieve my ultimate goal. As a result, I will dedicate no more than 25% of my trading account to longer term investments. These will be trades I expect to last over 1 month upwards of 1 year. The majority of my trades will last a few days to a few weeks.
The trading systems I have found/modified/developed will be noted as:
None – no system Will no longer use this.
Pangolin-Z – A short term reversal trading strategy not developed by me. Back testing and live testing indicate trades last approximately 3 days to 9 days. Current strategy.
BB Squeeze – A short term breakout trading strategy I have modified to suit my methods. Back testing indicates trades last approximately 5 days. Currently live testing.
Aroon Cross – A long term breakout trading strategy I have developed to suit my methods. Back testing indicates trades last 1 month upwards to 1 year. Currently live testing.
The Big Win – A higher risk short term options trading strategy I have developed to suit my methods. Currently undergoing analysis and won’t start live testing for a while if analysis is promising.
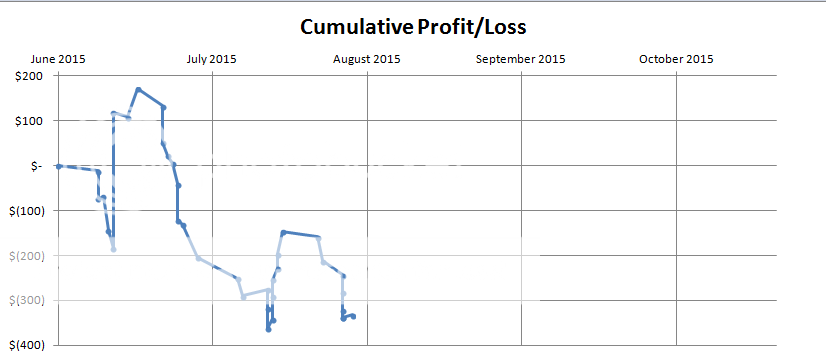
I will be keeping a chart showing my cumulative profit/loss as well as my equity curve in this post starting at the end of this month which will be updated each month. Since I will be adding to my trading account each month, the cumulative profit/loss curve will be more telling of if what I am doing is working. I will post the trades I enter and the reason for their entry in subsequent posts. I intend to post these weekly with the reasons for entering to help keep my trading disciplined.
Wish me luck!
Current target:
The first target I am setting for myself is to have one month with a positive return. I believe I will achieve that this month and will bring my account back close to break even from my undisciplined first month.
1. I do not want to spend my life working. I do not need a huge stack of cash to enjoy life, and would rather spend my time on hobbies where I am my own boss than at a high paying job.
2. I can manage my cash as well as “professional” brokers. The catalyst that began my journey was after watching my “professionally managed” $45,000 investment account at Charles Schwab continuously decline to a meager $3,000 between 2011 and 2015. I figured I can do at least that good, so I moved my funds over to an account I now manage and have started trading myself.
After a month of trading with no real plan and getting a feel for how it works, I realized that I can’t just wing it and do well. I have developed a few trading plans that I am now testing out and sticking to rigidly. Over time I may add more plans, evolve my current ones, etc., but there will always be a plan for the trade I am executing and it will be formed prior to executing it and it will be stuck to.
In order to achieve my ultimate goal of becoming financially independent, I am setting some smaller goals:
1. Cut my current monthly spending by a third. This should be easily doable by cooking more. By doing this I will be able to add approximately half my monthly paycheck into my trading account.
2. Lose no more than 5% of the starting value of my account in any month. In order to help achieve this I will:
a. Not risk any more than 1.5% and rarely any more than 1% of my account on any trade. While live testing new strategies, I will not risk more than half of this.
b. Follow my execution plans and wait for appropriate times to enter into trades. No trading just to be trading.
c. Not have any more than 5% of my starting account balance for each month at risk at any point in time. If a trade moves so my stop loss puts me above my entry, the trades risk drops to 0 and I can enter new positions.
d. Not add more than 3% of risk to my starting account balance for each month on any single day. This should limit my new positions for each day to approximately 2-4.
I will declare myself financially independent once one of the following occurs:
1. The average income I generate from trading exceeds my job income over a 6 month period.
2. The size of my trading account exceeds my typical monthly expenses by 100% and I have had 4 consecutive 3 month periods with gains averaging greater than 5% of my starting account balance that month and no losing 3 month period in this timeframe.
3. The size of my trading account exceeds my typical monthly expenses by 200%.
I will stop trading and accept that my life fate is to work like most people once one of the following occurs:
1. I have a 12 month period with a net loss on all closed trades.
2. I have 4 consecutive months of losing more than 5% of the starting value of my account that month.
3. I have a 3 month period with a net loss that is a direct result of violating the trading rules and systems I have set in place.
I have determined that a handful of long term and a larger number of short term trades will be the best and most practical way for me to achieve my ultimate goal. As a result, I will dedicate no more than 25% of my trading account to longer term investments. These will be trades I expect to last over 1 month upwards of 1 year. The majority of my trades will last a few days to a few weeks.
The trading systems I have found/modified/developed will be noted as:
None – no system Will no longer use this.
Pangolin-Z – A short term reversal trading strategy not developed by me. Back testing and live testing indicate trades last approximately 3 days to 9 days. Current strategy.
BB Squeeze – A short term breakout trading strategy I have modified to suit my methods. Back testing indicates trades last approximately 5 days. Currently live testing.
Aroon Cross – A long term breakout trading strategy I have developed to suit my methods. Back testing indicates trades last 1 month upwards to 1 year. Currently live testing.
The Big Win – A higher risk short term options trading strategy I have developed to suit my methods. Currently undergoing analysis and won’t start live testing for a while if analysis is promising.
I will be keeping a chart showing my cumulative profit/loss as well as my equity curve in this post starting at the end of this month which will be updated each month. Since I will be adding to my trading account each month, the cumulative profit/loss curve will be more telling of if what I am doing is working. I will post the trades I enter and the reason for their entry in subsequent posts. I intend to post these weekly with the reasons for entering to help keep my trading disciplined.
Wish me luck!
Current target:
The first target I am setting for myself is to have one month with a positive return. I believe I will achieve that this month and will bring my account back close to break even from my undisciplined first month.
Last edited: