I'll bet you probably never considered how international options trading can be! We know there are American options, which can be exercised at any time from when they are bought until their date of expiration (we call that "early exercise.") There are also European options, which cannot be exercised early, and can only be exercised on their expiration date. Well today we're going to learn about the "Greeks." This term should not be new to anybody who is already trading options. The reason is that they are so important, that unless you have a basic understanding of what they are, and how to use them, you are going to be trading with a serious disadvantage.
So what are these Greeks? Simply put, we can call them risk measurements, (sorry I had to throw in a little options humor there). Previously we learned that the theoretical value of an option can be determined by plugging some variables into the Black-Scholes formula. Well the Greeks tell an options trader the theoretical change in the options price given a change in one of the variables. They represent rates of change. For those of you familiar with the Calculus, you may recognize that the Greeks are really partial derivatives, but we won't dwell on that here. The variables that have Greeks associated with them are: stock price, time to expiration, projected volatility, and the risk free rate of return. The two other variables needed to price options using Black-Scholes, namely exercise price, and dividend rate, do not have associated Greeks.
This week we'll discuss some basic aspects of one of the most widely used of the Greeks. We'll follow up with more details and the rest of the Greeks later on.
Delta
The Delta of an option is a percentage that represents the change in the options price given a 1 point change in the price of the underlying stock. Notice that as the price of a stock increases, the price of a Call option will also increase (assuming all other things being equal.) On the other hand, the price of a Put option will decrease as the stock price increases. So Call option deltas will range from 0 to 100, while Put deltas range from -100 to 0 (the percentage sign is generally omitted.)
Calls that are very much out of the money (OTM) will have very small deltas. In other words, a small change in stock price will not have much of an affect, whereas a deep in the money (ITM) Call will move very close to the same amount as the change in the stock. At the money (ATM) Calls have deltas of about 50, meaning that for small changes in the stock price, the Call will change by about half of the stock price of change.
Put options are similar, but the signs are reversed. Okay, just to be sure, I'll spell it out. Puts that are very much OTM have deltas close to 0. Deep ITM Puts have deltas close to -1, and ATM Puts have deltas of about -50.
Here are some examples. The prices of the options with the stock equal to 100 are given. Notice how the option prices change with the stock price at 100.5 and at 99. It will help your understanding of this important topic if you can independently verify the numbers in the last 2 columns.

Notice that the Call delta minus the Put delta for a given strike price equals 100. This is usually true although the difference may be slightly greater. It will never be less than 100.
Another important and useful way of looking at delta, is to consider it as an equivalent stock position (ESP.) Using this approach, we will be able to take a combination of stock and options and know that it will have the characteristics of a given number of shares of stock, hence, an ESP.
We just need a couple of rules to be able to do this. First, stock always has a delta of 100. So if we're long 300 shares we have 300 deltas, if we're short 800 shares we have -800 deltas. Since an option contract represents 100 shares of stock, to keep the accounting straight, we need to think of stock in lots of 100 shares. In the preceding example, we would think of it as 3 lots of 100 shares times 100 deltas to get 300.
Second, for each option position, we multiply the number of contracts by the delta. Keep in mind that the number of contracts will be positive if we're long the options and negative if we're short. So if we're long 10 of the Feb 85 Calls, we have +10 x +90 = +900 deltas. On the other hand, if we're short 5 of the Feb 120 Puts, then we have -5 x -86 = +430 deltas. Remember, a minus times a minus is a plus. Finally, to arrive at our ESP, we add up all the options and stock deltas in our position.
Believe me, it sounds a lot worse than it is. Most options trading platforms show you the value of the deltas, and some of the better ones, will calculate the ESP for you. There are also many commercially available software products that are quite reasonably priced.
Let's look at a hypothetical position:

The bottom line is that even though this position looks pretty complicated, it boils down to just being long the equivalent of about 180 shares of stock. That's a lot more manageable.
In addition to the 2 ways that we've seen to interpret the delta, there is a third. The delta of a Call, can be thought of as the probability that the stock will be ITM at expiration. This is not mathematically precise, but it is widely used and is considered a decent estimate. So based on the fact that the Feb 85 Call has a delta of 90, we can think that there is a 90% chance that the stock will be above 85 at the expiration of the February options. This is a sometimes useful tool, but be careful when using this information, it's based on a model, it's based on assumptions, and it's not mathematically precise.
Gamma
Well, if you thought delta was fun, you're going to love gamma! Gamma represents the change in delta, given a one point change in the underlying stock. It's different from the other Greeks in that it represents change in another Greek (delta) as opposed to a change in the options value. For the mathematicians out there, while the other Greeks are partial derivatives of the options price with respect to the corresponding variable, gamma is the second partial derivative of an options price with respect to a change in the underlying stock. Looking at some examples will bring this discussion back into English.
Let's assume that XYZ stock is trading at $25. We would expect the April 25 Call to have a delta of about 50. If the gamma is equal to, let's say 6, then we would expect the delta of the Call to be 56 if the stock increases to $26 and 44 if the stock decreased to $24. Similarly, the April 25 Put would have a delta of -50 with the stock at $25. An increase to $26 would result in a delta of -50 + 6 = -44 and a decrease to $24 would result in a delta of -56. There are 3 interesting things to note from this.
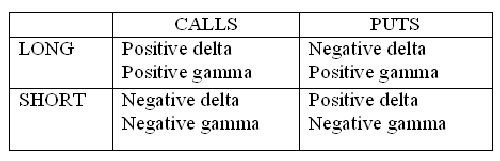
First, the gammas of both Puts and Calls are positive, whereas the deltas of Calls are positive and Puts are negative. Second, the gammas of the corresponding Put and Call are equal. This is always the case and is a function of most option pricing models. Next, note that if gamma stayed at 6, the delta of the Call option would eventually exceed 100 if the stock price kept increasing. We'd have the same problem on the downside, if the stock price continued to decrease, eventually the delta would turn negative. So we can surmise that the gamma cannot be constant. In fact, gamma attains its maximum value when the option is ATM. As the option goes ITM or OTM, the gamma decreases to 0. Professional traders also look at the rate of change of the gamma, affectionately referred to as the "gamma of the gamma." Don't worry, I won't mention that again.
Note, that like delta, we can come up with a position gamma, simply by summing the gammas of each of the options in the position. So if we take last week's hypothetical example and add gammas, we get:
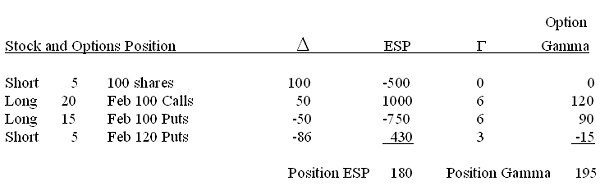
The final points I want to make about gamma now is that stock has no gamma, ie, it is always 0. Also, while Puts and Calls always have positive gammas, when the options are short, their gammas will be negative. If you have software that is keeping track of your Greek positions, it will automatically take care of the positive and negative signs and give you a proper total. However, if you're keeping track of your gamma position by hand, it is imperative that the correct signs be used. Until it becomes second nature, perhaps this table will help to keep things straight:
Vega
Right away, we have a problem with this fake Greek. Vega may have been a Chevy back in the 70's, but was never an authentic Greek letter! However, it is thoroughly ingrained in the language of options, although the politically correct crowd is trying to change the name to either kappa or tau, both of which are authentic letters of the Greek alphabet. I'm old fashioned so we'll continue to use vega here, but if you see kappa or tau somewhere else, you'll know what they're talking about.
Vega is the change in an options value that results from a change in volatility. I know that we haven't talked much about volatility yet, but it's one of the most important variables in the determination of an options theoretical price and we will discuss it at length at a later date.
Vega is expressed in dollars per a 1 percentage point change in volatility. For example, assume the theoretical value of the XYZ March 25 Put is $4.00 with a volatility of 30%, and a vega of .25. If nothing else changes but the volatility increases to 31%, we would expect the value of the Put to increase to $4.25. Likewise, if the volatility decreased to 29%, we would expect the Put to decrease to $3.75.
Like gamma, the vegas of long Puts and Calls are positive and the vegas of short options are negative. Also like gamma, the vegas of a corresponding Put and Call will be equal. And again, like gamma, stock does not have any vega associated with it. Unlike gamma however, vegas don't change very much for a given volatility, unless the stock price moves a considerable distance. Since changes in volatility will be more pronounced when there is more time to expiration, vegas will decrease as the time to expiration approaches. Also, bear in mind that the vegas for the ATM options are usually greater than the vegas for ITM and OTM options.
Theta
Theta represents the change in an options value based on a one day decrease in the amount of time until expiration. It measures the rate of time decay of an option and is measured in dollars per day. Assume the XYZ April 35 Call has a theoretical value of $6.00 with 90 days to go until expiration and a theta of .06. Tomorrow with only 89 days to expiration, the Call will be worth $5.94, assuming nothing else changes. It seems rather obvious that both Puts and Calls have negative thetas. Just remember that time is an enemy of long options and a friend to short options. Not as obvious is the fact that the Put and Call thetas are different, ie, they decay at different rates. Calls typically decay faster than Puts and therefore have higher thetas. Also, long term options have very low thetas, while near term thetas are large.
Higher volatility options will have higher thetas than lower volatility options and generally the ATM options will be higher than either the OTM or ITM options. Like our friends gamma and vega, stock does not have any theta associated with it.
Rho
Alas, we have come to the last of our Greeks. Rho represents the change in an options theoretical value based on a change in the risk free rate of return. It is measured in dollars per 1 percentage point change in the risk free rate. Calls increase as the risk free rate increases, while Puts decrease. So rho for Calls is positive and negative for Puts. For example, assume the XYZ July 45 Put has a theoretical value of $5.70 and a rho of -.12. Then if nothing else changes, but the risk free rate goes to 6% the Put will be worth $5.58. Likewise, if the rate declines to 4%, the Put will increase in value to $5.82. In times of low interest rates or stable interest rates, rho was not considered one of the more important Greeks. However, if you're trading LEAPS or in a situation where the rate is changing often, then rho can be very important. In fact when I was trading on the floor of the Amex in the 1990's there was a time when interest rates were in the 12-13% range. Rho was very important.
So what are these Greeks? Simply put, we can call them risk measurements, (sorry I had to throw in a little options humor there). Previously we learned that the theoretical value of an option can be determined by plugging some variables into the Black-Scholes formula. Well the Greeks tell an options trader the theoretical change in the options price given a change in one of the variables. They represent rates of change. For those of you familiar with the Calculus, you may recognize that the Greeks are really partial derivatives, but we won't dwell on that here. The variables that have Greeks associated with them are: stock price, time to expiration, projected volatility, and the risk free rate of return. The two other variables needed to price options using Black-Scholes, namely exercise price, and dividend rate, do not have associated Greeks.
This week we'll discuss some basic aspects of one of the most widely used of the Greeks. We'll follow up with more details and the rest of the Greeks later on.
Delta
The Delta of an option is a percentage that represents the change in the options price given a 1 point change in the price of the underlying stock. Notice that as the price of a stock increases, the price of a Call option will also increase (assuming all other things being equal.) On the other hand, the price of a Put option will decrease as the stock price increases. So Call option deltas will range from 0 to 100, while Put deltas range from -100 to 0 (the percentage sign is generally omitted.)
Calls that are very much out of the money (OTM) will have very small deltas. In other words, a small change in stock price will not have much of an affect, whereas a deep in the money (ITM) Call will move very close to the same amount as the change in the stock. At the money (ATM) Calls have deltas of about 50, meaning that for small changes in the stock price, the Call will change by about half of the stock price of change.
Put options are similar, but the signs are reversed. Okay, just to be sure, I'll spell it out. Puts that are very much OTM have deltas close to 0. Deep ITM Puts have deltas close to -1, and ATM Puts have deltas of about -50.
Here are some examples. The prices of the options with the stock equal to 100 are given. Notice how the option prices change with the stock price at 100.5 and at 99. It will help your understanding of this important topic if you can independently verify the numbers in the last 2 columns.

Notice that the Call delta minus the Put delta for a given strike price equals 100. This is usually true although the difference may be slightly greater. It will never be less than 100.
Another important and useful way of looking at delta, is to consider it as an equivalent stock position (ESP.) Using this approach, we will be able to take a combination of stock and options and know that it will have the characteristics of a given number of shares of stock, hence, an ESP.
We just need a couple of rules to be able to do this. First, stock always has a delta of 100. So if we're long 300 shares we have 300 deltas, if we're short 800 shares we have -800 deltas. Since an option contract represents 100 shares of stock, to keep the accounting straight, we need to think of stock in lots of 100 shares. In the preceding example, we would think of it as 3 lots of 100 shares times 100 deltas to get 300.
Second, for each option position, we multiply the number of contracts by the delta. Keep in mind that the number of contracts will be positive if we're long the options and negative if we're short. So if we're long 10 of the Feb 85 Calls, we have +10 x +90 = +900 deltas. On the other hand, if we're short 5 of the Feb 120 Puts, then we have -5 x -86 = +430 deltas. Remember, a minus times a minus is a plus. Finally, to arrive at our ESP, we add up all the options and stock deltas in our position.
Believe me, it sounds a lot worse than it is. Most options trading platforms show you the value of the deltas, and some of the better ones, will calculate the ESP for you. There are also many commercially available software products that are quite reasonably priced.
Let's look at a hypothetical position:

The bottom line is that even though this position looks pretty complicated, it boils down to just being long the equivalent of about 180 shares of stock. That's a lot more manageable.
In addition to the 2 ways that we've seen to interpret the delta, there is a third. The delta of a Call, can be thought of as the probability that the stock will be ITM at expiration. This is not mathematically precise, but it is widely used and is considered a decent estimate. So based on the fact that the Feb 85 Call has a delta of 90, we can think that there is a 90% chance that the stock will be above 85 at the expiration of the February options. This is a sometimes useful tool, but be careful when using this information, it's based on a model, it's based on assumptions, and it's not mathematically precise.
Gamma
Well, if you thought delta was fun, you're going to love gamma! Gamma represents the change in delta, given a one point change in the underlying stock. It's different from the other Greeks in that it represents change in another Greek (delta) as opposed to a change in the options value. For the mathematicians out there, while the other Greeks are partial derivatives of the options price with respect to the corresponding variable, gamma is the second partial derivative of an options price with respect to a change in the underlying stock. Looking at some examples will bring this discussion back into English.
Let's assume that XYZ stock is trading at $25. We would expect the April 25 Call to have a delta of about 50. If the gamma is equal to, let's say 6, then we would expect the delta of the Call to be 56 if the stock increases to $26 and 44 if the stock decreased to $24. Similarly, the April 25 Put would have a delta of -50 with the stock at $25. An increase to $26 would result in a delta of -50 + 6 = -44 and a decrease to $24 would result in a delta of -56. There are 3 interesting things to note from this.
First, the gammas of both Puts and Calls are positive, whereas the deltas of Calls are positive and Puts are negative. Second, the gammas of the corresponding Put and Call are equal. This is always the case and is a function of most option pricing models. Next, note that if gamma stayed at 6, the delta of the Call option would eventually exceed 100 if the stock price kept increasing. We'd have the same problem on the downside, if the stock price continued to decrease, eventually the delta would turn negative. So we can surmise that the gamma cannot be constant. In fact, gamma attains its maximum value when the option is ATM. As the option goes ITM or OTM, the gamma decreases to 0. Professional traders also look at the rate of change of the gamma, affectionately referred to as the "gamma of the gamma." Don't worry, I won't mention that again.
Note, that like delta, we can come up with a position gamma, simply by summing the gammas of each of the options in the position. So if we take last week's hypothetical example and add gammas, we get:

The final points I want to make about gamma now is that stock has no gamma, ie, it is always 0. Also, while Puts and Calls always have positive gammas, when the options are short, their gammas will be negative. If you have software that is keeping track of your Greek positions, it will automatically take care of the positive and negative signs and give you a proper total. However, if you're keeping track of your gamma position by hand, it is imperative that the correct signs be used. Until it becomes second nature, perhaps this table will help to keep things straight:

Vega
Right away, we have a problem with this fake Greek. Vega may have been a Chevy back in the 70's, but was never an authentic Greek letter! However, it is thoroughly ingrained in the language of options, although the politically correct crowd is trying to change the name to either kappa or tau, both of which are authentic letters of the Greek alphabet. I'm old fashioned so we'll continue to use vega here, but if you see kappa or tau somewhere else, you'll know what they're talking about.
Vega is the change in an options value that results from a change in volatility. I know that we haven't talked much about volatility yet, but it's one of the most important variables in the determination of an options theoretical price and we will discuss it at length at a later date.
Vega is expressed in dollars per a 1 percentage point change in volatility. For example, assume the theoretical value of the XYZ March 25 Put is $4.00 with a volatility of 30%, and a vega of .25. If nothing else changes but the volatility increases to 31%, we would expect the value of the Put to increase to $4.25. Likewise, if the volatility decreased to 29%, we would expect the Put to decrease to $3.75.
Like gamma, the vegas of long Puts and Calls are positive and the vegas of short options are negative. Also like gamma, the vegas of a corresponding Put and Call will be equal. And again, like gamma, stock does not have any vega associated with it. Unlike gamma however, vegas don't change very much for a given volatility, unless the stock price moves a considerable distance. Since changes in volatility will be more pronounced when there is more time to expiration, vegas will decrease as the time to expiration approaches. Also, bear in mind that the vegas for the ATM options are usually greater than the vegas for ITM and OTM options.
Theta
Theta represents the change in an options value based on a one day decrease in the amount of time until expiration. It measures the rate of time decay of an option and is measured in dollars per day. Assume the XYZ April 35 Call has a theoretical value of $6.00 with 90 days to go until expiration and a theta of .06. Tomorrow with only 89 days to expiration, the Call will be worth $5.94, assuming nothing else changes. It seems rather obvious that both Puts and Calls have negative thetas. Just remember that time is an enemy of long options and a friend to short options. Not as obvious is the fact that the Put and Call thetas are different, ie, they decay at different rates. Calls typically decay faster than Puts and therefore have higher thetas. Also, long term options have very low thetas, while near term thetas are large.
Higher volatility options will have higher thetas than lower volatility options and generally the ATM options will be higher than either the OTM or ITM options. Like our friends gamma and vega, stock does not have any theta associated with it.
Rho
Alas, we have come to the last of our Greeks. Rho represents the change in an options theoretical value based on a change in the risk free rate of return. It is measured in dollars per 1 percentage point change in the risk free rate. Calls increase as the risk free rate increases, while Puts decrease. So rho for Calls is positive and negative for Puts. For example, assume the XYZ July 45 Put has a theoretical value of $5.70 and a rho of -.12. Then if nothing else changes, but the risk free rate goes to 6% the Put will be worth $5.58. Likewise, if the rate declines to 4%, the Put will increase in value to $5.82. In times of low interest rates or stable interest rates, rho was not considered one of the more important Greeks. However, if you're trading LEAPS or in a situation where the rate is changing often, then rho can be very important. In fact when I was trading on the floor of the Amex in the 1990's there was a time when interest rates were in the 12-13% range. Rho was very important.
Last edited by a moderator:
