With the recent rise in volatility, there has been a lot of talk about a potential equity market crash. Many investors are nervous about when, not if, this crash will occur and are looking for some protection for their stock portfolios. Closing out your stock positions is an option, but many stocks pay dividends that the investors do not want to relinquish even when facing the threat of, or, during a crash. Another reason for holding on to a stock position is to avoid tax ramifications on profitable sales of securities.
The most common protection that traders/investors seek is to buy puts on stocks they are holding. The value of the put will increase as the price of the underlying stock decreases thus covering the losses in the stock position. This is easy but also very expensive as you will have to pay a premium for every put you buy for every stock that you insure.
Fortunately, there is a less expensive way to protect a portfolio. You can use the index futures contracts as a hedge for your stock holdings. Selling a future is easy if you know how they work, and selling futures is also allowed in certain IRA accounts.
Before you go out and sell the ES (the S&P 500 E-Mini futures Contract), you need to know how many contracts are needed to hedge your account. The ES is the equivalent of trading 500 shares of the SPY but at a fraction of the margin cost. At the time of my writing this article, the SPY is trading at about $277 per share. 500 shares would cost $138,500. Comparatively, the overnight margin requirement for the ES is only $6160.
You need to analyze your portfolio and determine the Beta Weighting. Beta is a measure of volatility versus the S&P 500 Index. The index has a Beta of one. If your stock’s Beta is 1.5, then it is 50% more volatile than the index. On average, (though not every day), when the index moves one percent your stock should move about one and a half percent in the same direction.
There are several easy steps to Beta Weight your portfolio:
First, you can multiply the amount you have invested in each stock by the Beta of that stock. Let’s take the sample portfolio below.

Fig 1
When you total the portfolio, there is $49,055 invested. Adding the result of the individual Betas multiplied by the individual investments we have $48,605.55. Dividing that by the total amount invested gives us a Beta Weight of 0.99. This portfolio has nearly the same volatility as the S&P 500, so when the market moves in a particular direction, this portfolio should move the same and in the same direction.
Using your analysis of the S&P Index, you could determine how much you expect the markets to fall to their demand. When you figure out the expected return, you could sell futures contracts to cover your losses in your stocks. In the sample portfolio, the 1300 shares have a 0.99 beta. To cover the potential losses, the investor would sell two or three S&P 500 eMini contracts to be market neutral, (1300 shares x 0.99 = 1287 and each eMini = 500 SPY shares). Two may be sufficient and three would actually profit when the market drops.
Even mutual funds have a beta, so the same can be done for a portfolio or 401k that contains mutual funds. This can usually be found on most financial websites.
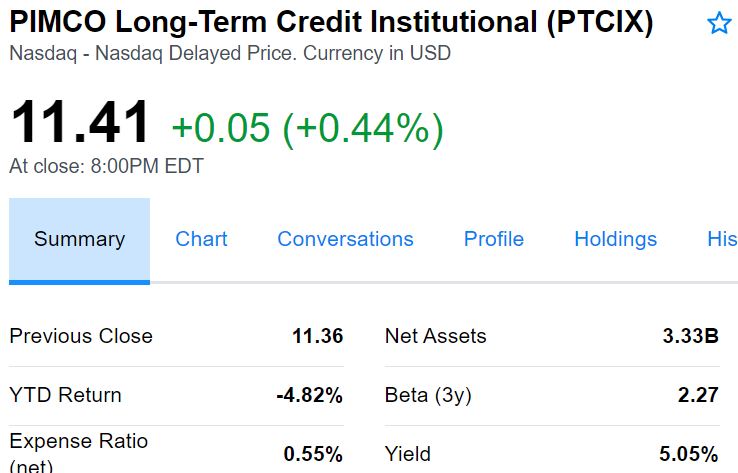
Fig 2
Once you have found the individual betas, calculate the portfolio’s total beta using the method I mentioned previously. I have selected several mutual funds from different companies to create a hypothetical portfolio below.
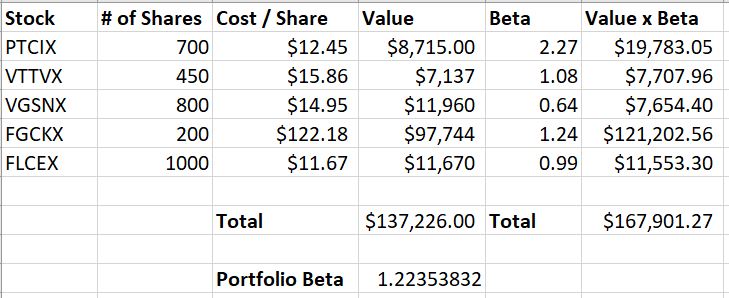
Fig 3
As you can see, this portfolio’s beta is 1.22 and consists of 3150 shares. This means that the investor needs insurance for 3843 shares. If they were to sell S&P 500 eMini futures, seven contracts would provide insurance for the portfolio. The problem is that the margin requirement for each contract is $6160 so the insurance would cost $43,120 to insure a $137,226 portfolio. This hardly seems efficient.
Fortunately, there are additional ways to trade the S&P futures that will offer a more cost-efficient method with similar protections. I had previously mentioned that most investors will trade options to hedge a position. Specifically, they will purchase puts on shares that they own. This works for individual stocks as they are optionable. Mutual funds do not have options available however.
Since we were planning to use the S&P 500 derivatives to hedge a portfolio, we can instead use the options on the futures. This will greatly reduce the cost of the insurance for our portfolio but still provide the same coverage.
Looking at the S&P 500 eMinis options, I am using a strike price below the current price level of 2770 for the start of the hedge. You will also notice that I am using the March 2019 contract and options instead of the current July one. This is because when you trade options, you must be aware of time decay and also want to have enough time for the position to cover your hedge. If you do not buy enough time, you will lose premium and also may be forced to roll over your position which results in additional commissions.
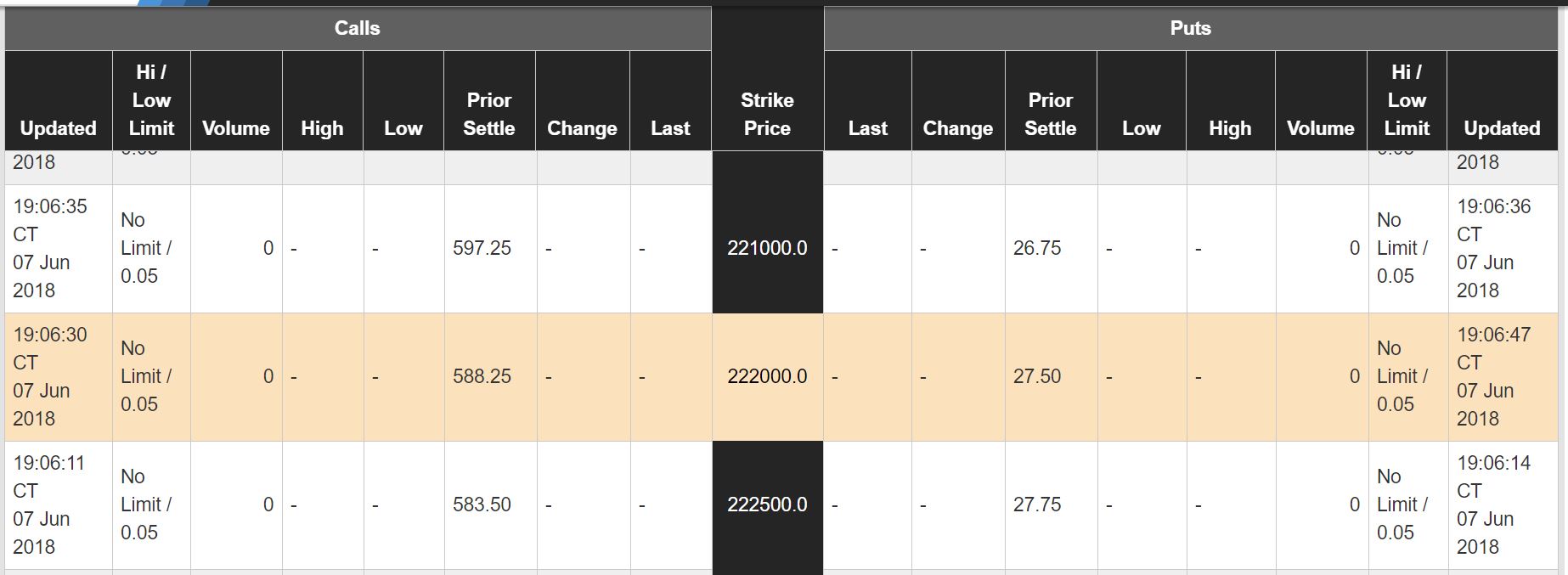
Fig 4
So, the puts would cost approximately $27.50 for each eMini we want. This would be a total cost of $9,625, or 7% of the value of the portfolio. For the cost calculation, you need to understand how the futures and the options on those futures are priced. Remember that the S&P 500 eMini futures contract equals 500 SPY. This portfolio would need to cover losses in 3800 shares so seven contracts should work.
This hedge is still less expensive than buying individual puts on stock, shorting the SPY, selling the ES (S&P 500 eMini), or simply holding on. As you can see, there are several additional factors that you must be aware of. You need to know a little about options as you may want to buy a different put option due to pricing. You can also look to do the hedge in a retirement account such as an IRA so that there are different tax ramifications.
Even more important is knowing when to put on the hedge and when to remove it. You will need to know the core strategy of market timing to learn when your portfolio is vulnerable and when to remove the hedge to let your portfolio grow.
Brandon Wendell can be contacted on this link: Brandon Wendell
The most common protection that traders/investors seek is to buy puts on stocks they are holding. The value of the put will increase as the price of the underlying stock decreases thus covering the losses in the stock position. This is easy but also very expensive as you will have to pay a premium for every put you buy for every stock that you insure.
Fortunately, there is a less expensive way to protect a portfolio. You can use the index futures contracts as a hedge for your stock holdings. Selling a future is easy if you know how they work, and selling futures is also allowed in certain IRA accounts.
Before you go out and sell the ES (the S&P 500 E-Mini futures Contract), you need to know how many contracts are needed to hedge your account. The ES is the equivalent of trading 500 shares of the SPY but at a fraction of the margin cost. At the time of my writing this article, the SPY is trading at about $277 per share. 500 shares would cost $138,500. Comparatively, the overnight margin requirement for the ES is only $6160.
You need to analyze your portfolio and determine the Beta Weighting. Beta is a measure of volatility versus the S&P 500 Index. The index has a Beta of one. If your stock’s Beta is 1.5, then it is 50% more volatile than the index. On average, (though not every day), when the index moves one percent your stock should move about one and a half percent in the same direction.
There are several easy steps to Beta Weight your portfolio:
First, you can multiply the amount you have invested in each stock by the Beta of that stock. Let’s take the sample portfolio below.

Fig 1
When you total the portfolio, there is $49,055 invested. Adding the result of the individual Betas multiplied by the individual investments we have $48,605.55. Dividing that by the total amount invested gives us a Beta Weight of 0.99. This portfolio has nearly the same volatility as the S&P 500, so when the market moves in a particular direction, this portfolio should move the same and in the same direction.
Using your analysis of the S&P Index, you could determine how much you expect the markets to fall to their demand. When you figure out the expected return, you could sell futures contracts to cover your losses in your stocks. In the sample portfolio, the 1300 shares have a 0.99 beta. To cover the potential losses, the investor would sell two or three S&P 500 eMini contracts to be market neutral, (1300 shares x 0.99 = 1287 and each eMini = 500 SPY shares). Two may be sufficient and three would actually profit when the market drops.
Even mutual funds have a beta, so the same can be done for a portfolio or 401k that contains mutual funds. This can usually be found on most financial websites.

Fig 2
Once you have found the individual betas, calculate the portfolio’s total beta using the method I mentioned previously. I have selected several mutual funds from different companies to create a hypothetical portfolio below.

Fig 3
As you can see, this portfolio’s beta is 1.22 and consists of 3150 shares. This means that the investor needs insurance for 3843 shares. If they were to sell S&P 500 eMini futures, seven contracts would provide insurance for the portfolio. The problem is that the margin requirement for each contract is $6160 so the insurance would cost $43,120 to insure a $137,226 portfolio. This hardly seems efficient.
Fortunately, there are additional ways to trade the S&P futures that will offer a more cost-efficient method with similar protections. I had previously mentioned that most investors will trade options to hedge a position. Specifically, they will purchase puts on shares that they own. This works for individual stocks as they are optionable. Mutual funds do not have options available however.
Since we were planning to use the S&P 500 derivatives to hedge a portfolio, we can instead use the options on the futures. This will greatly reduce the cost of the insurance for our portfolio but still provide the same coverage.
Looking at the S&P 500 eMinis options, I am using a strike price below the current price level of 2770 for the start of the hedge. You will also notice that I am using the March 2019 contract and options instead of the current July one. This is because when you trade options, you must be aware of time decay and also want to have enough time for the position to cover your hedge. If you do not buy enough time, you will lose premium and also may be forced to roll over your position which results in additional commissions.

Fig 4
So, the puts would cost approximately $27.50 for each eMini we want. This would be a total cost of $9,625, or 7% of the value of the portfolio. For the cost calculation, you need to understand how the futures and the options on those futures are priced. Remember that the S&P 500 eMini futures contract equals 500 SPY. This portfolio would need to cover losses in 3800 shares so seven contracts should work.
This hedge is still less expensive than buying individual puts on stock, shorting the SPY, selling the ES (S&P 500 eMini), or simply holding on. As you can see, there are several additional factors that you must be aware of. You need to know a little about options as you may want to buy a different put option due to pricing. You can also look to do the hedge in a retirement account such as an IRA so that there are different tax ramifications.
Even more important is knowing when to put on the hedge and when to remove it. You will need to know the core strategy of market timing to learn when your portfolio is vulnerable and when to remove the hedge to let your portfolio grow.
Brandon Wendell can be contacted on this link: Brandon Wendell
Last edited by a moderator:
