What Is The Risk Of Ruin?
Please excuse me if I start off a little technical in this article. There is nothing complicated about the risk of ruin concept but it does require a quick calculation.
Simply stated, the risk of ruin is the percentage probability that a trader's account balance will reach zero. This will either result in the trader ceasing to speculate on the financial markets, or having to stump up another chunk of capital in an attempt to make back the first tranche before making net profits.
Having a solid trading strategy which is applied with discipline is clearly crucial, however understanding your probability of success or failure given certain actions must be more so. By using the risk of ruin formula a trader can optimise his risk per trade to minimise the probability of going under.
Edge is the percentage advantage that the trading strategy has over a randomly selected group of "nonsense" trades. For example, if I place 10,000 trades and 50% of the time the market falls and 50% of the time it rises (when I thought it would rise every time) the results would show that my strategy had an edge of zero%.
However, if my predictions are accurate 51% of the time then I have an edge of 1%.
Capital units are the number of units of money that you have to risk. For example, if you have £1,000 in your trading account and risk £50 on every trade, you have a total of 20 capital units (1,000 / 50).
The Risk Per Trade
The most important thing to consider in calculating the risk of ruin for your trading is your "edge". If your edge is zero and your trades are no better than darts thrown at a financial newspaper by a monkey then you should not trade at all. Assuming however that you are able to make at least slightly intelligent decisions it should be greater than zero.
Let us conservatively assume the hypothetical case of a trader with a 5% edge over randomness. The chart below shows the probability of depleting his account to zero assuming a range of units of capital from 1 unit to 100.
As the number of units of capital increases, the probability of losing all of the funds in his account decreases towards zero.
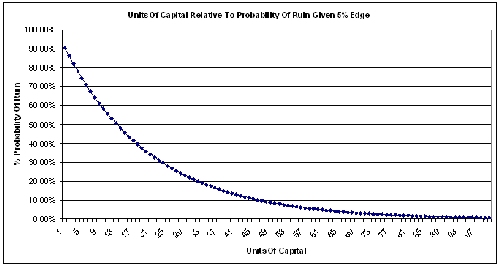
What this means in practical terms is that one should sub divide one's account into anything up to 100 individual units of capital and risk no more than one unit per trade.
How And Where To Trade
A trader with £1,000 at his disposal should, if being conservative, risk no more than £10 on each transaction. This may seem like a very small amount but don't worry. By following a good strategy you will increase your capital at a solid rate until you have many times more money and are trading in far larger size.
As risking smaller amounts (such as £10 or £20 per trade) is not feasible through the mainstream brokers I would advocate starting off with the greater leverage and lower risk that fixed odds financial betting offers.
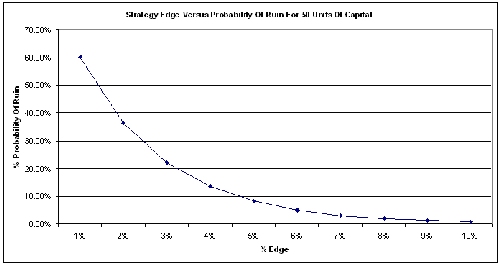
As you increase your edge, you can reduce the number of units of capital you need because (see chart below) a more skilled trader with a better edge has a far lower probability of ruin. This means that each trade will be bigger and in turn lead to greater profits.
Optimal Risk Size Using the Kelly Criterion
Traders often ask how much they should risk on each transaction in order to ensure the highest possible returns and the lowest probability of depleting their account to zero. The problem is that the more you risk, the higher your potential yield, but this is coupled with greater potential for significant loss.
In allocating capital to a trading or betting strategy a trader can significantly improve his performance by ensuring that he risks the optimal amount per transaction.
What Is The Kelly Criterion?
The Kelly Criterion is a formula for calculating the percentage of a trader's total risk capital that he should stake given his probability of winning and the odds offered on the bet.
The formula was originally published by J.L Kelly in 1956 and published in the Bell System Technical Journal. It was devised for minimising noise over long-distance telephone lines but it's application to the speculator, whose market information may contain errors ("noise"), was quickly realised.
There are a number of advantages to the Kelly Criterion including:
Calculating Bet Size
Now for a little bit of simple maths, to explain and demonstrate the formula.
Anyone familiar with Microsoft Excel should be able to do the calculation in a spreadsheet (I have pasted the Excel formula for the example below in a footnote to save you time).
I recently placed a EUR/USD bet and considered that my probability of winning was at very least 30% and the odds quoted on the site were 3/1 =((3*30%)-70%)/3
I punched the numbers into my Kelly Criterion spreadsheet which told me that I ought to risk 6.67% of my available capital on this bet. If my estimation of the minimum probability of winning was right (and I am always very conservative in my guesses so I usually do well at this) then this was a great bet.
Even by winning such a bet just 30% of the time, one could make substantial profits over the course of many bets.
Risk Is A Matter Of Taste
The Kelly Criterion is mathematically optimal for picking risk size per bet but it does have a drawback that many traders like to adjust for.
A feature of it is that it provides a "mirror" probability of losing a given percentage of your capital. When a series of bets are placed using the Criterion it gives the trader a 50% chance of at some time reducing his capital to 50% of the starting amount, a 40% chance or reducing it to 40%, a 10% chance of reducing it to 10% and so on. While he will probably make the losses back if he uses the model correctly this is just too much risk for many traders.
The solution to this is to calculate the risk amount per bet using the Kelly Criterion and then to divide it by a number depending on your risk appetite. The reduction in bet size does not decrease the long run returns linearly. For example, betting at 50% of the suggested amount will still pay the trader 75% of the returns that risking the full Kelly bet amount would have done but with far less volatility.
Why And Where To Use The Kelly Criterion
The Kelly Criterion provides the mathematically optimal balance of risk versus reward. Some traders are more concerned with risk and others with reward.
Betting more than the Kelly percentage is never optimal and will probably lead to long term depletion of capital and many traders are most comfortable at 50% or even 33.33% of the Kelly bet size. I am a fairly aggressive trader so choose to bet 100% of the Kelly size relative to the funds in each of my trading accounts.
If you have a tougher time determining the probability of success for each bet you make then Kelly betting is not for you. It is predicated on the ability to pick 'good bets'. You may however be interested in considering risk diversification and bet size in light of a model which does not require such knowledge. If so, see my article here: Beating The Risk Of Ruin.
Kelly betting is best deployed in trading scenarios where the stake and payout are known in advance. My interest in Kelly bet sizes is that the model is perfect for fixed odds financial betting and lends itself perfectly to Binarys, One Touches, No Touches, Time Switches and their respective ranges.
Please excuse me if I start off a little technical in this article. There is nothing complicated about the risk of ruin concept but it does require a quick calculation.
Simply stated, the risk of ruin is the percentage probability that a trader's account balance will reach zero. This will either result in the trader ceasing to speculate on the financial markets, or having to stump up another chunk of capital in an attempt to make back the first tranche before making net profits.
Having a solid trading strategy which is applied with discipline is clearly crucial, however understanding your probability of success or failure given certain actions must be more so. By using the risk of ruin formula a trader can optimise his risk per trade to minimise the probability of going under.
Risk of ruin = ((1 - Edge) / (1 + Edge)) ^ Capital units
Where ^ denotes 'to the power of'
Edge is the percentage advantage that the trading strategy has over a randomly selected group of "nonsense" trades. For example, if I place 10,000 trades and 50% of the time the market falls and 50% of the time it rises (when I thought it would rise every time) the results would show that my strategy had an edge of zero%.
However, if my predictions are accurate 51% of the time then I have an edge of 1%.
Capital units are the number of units of money that you have to risk. For example, if you have £1,000 in your trading account and risk £50 on every trade, you have a total of 20 capital units (1,000 / 50).
The Risk Per Trade
The most important thing to consider in calculating the risk of ruin for your trading is your "edge". If your edge is zero and your trades are no better than darts thrown at a financial newspaper by a monkey then you should not trade at all. Assuming however that you are able to make at least slightly intelligent decisions it should be greater than zero.
Let us conservatively assume the hypothetical case of a trader with a 5% edge over randomness. The chart below shows the probability of depleting his account to zero assuming a range of units of capital from 1 unit to 100.
As the number of units of capital increases, the probability of losing all of the funds in his account decreases towards zero.

What this means in practical terms is that one should sub divide one's account into anything up to 100 individual units of capital and risk no more than one unit per trade.
How And Where To Trade
A trader with £1,000 at his disposal should, if being conservative, risk no more than £10 on each transaction. This may seem like a very small amount but don't worry. By following a good strategy you will increase your capital at a solid rate until you have many times more money and are trading in far larger size.
As risking smaller amounts (such as £10 or £20 per trade) is not feasible through the mainstream brokers I would advocate starting off with the greater leverage and lower risk that fixed odds financial betting offers.
As you increase your edge, you can reduce the number of units of capital you need because (see chart below) a more skilled trader with a better edge has a far lower probability of ruin. This means that each trade will be bigger and in turn lead to greater profits.

Optimal Risk Size Using the Kelly Criterion
Traders often ask how much they should risk on each transaction in order to ensure the highest possible returns and the lowest probability of depleting their account to zero. The problem is that the more you risk, the higher your potential yield, but this is coupled with greater potential for significant loss.
In allocating capital to a trading or betting strategy a trader can significantly improve his performance by ensuring that he risks the optimal amount per transaction.
What Is The Kelly Criterion?
The Kelly Criterion is a formula for calculating the percentage of a trader's total risk capital that he should stake given his probability of winning and the odds offered on the bet.
The formula was originally published by J.L Kelly in 1956 and published in the Bell System Technical Journal. It was devised for minimising noise over long-distance telephone lines but it's application to the speculator, whose market information may contain errors ("noise"), was quickly realised.
There are a number of advantages to the Kelly Criterion including:
- Assuming (and one must be careful here) that money and bet sizes are continuously divisible, use of the formula leads to a zero risk of ruin.
- It enables the trader to adjust his risk size for every transaction in order to allocate more capital to higher probability events than to lower. Thus capitalising on the best bets available.
- It is guaranteed to maximise profit potential and minimise ruin given the odds and the probability of winning.
Calculating Bet Size
Now for a little bit of simple maths, to explain and demonstrate the formula.
Anyone familiar with Microsoft Excel should be able to do the calculation in a spreadsheet (I have pasted the Excel formula for the example below in a footnote to save you time).
f* = bp - q / b
f* is the percentage of the available capital to risk
b represents the odds received on the bet (for example, 2/1 would be represented as 2)
p is the probability of winning the bet. This may require some guess work but more experienced traders are often good at figuring their percentage probability of being right. It just takes practice.
q is the probability of losing the bet (100% - p). So, if you have a 70% chance of winning, q would be 30%.
I recently placed a EUR/USD bet and considered that my probability of winning was at very least 30% and the odds quoted on the site were 3/1 =((3*30%)-70%)/3
I punched the numbers into my Kelly Criterion spreadsheet which told me that I ought to risk 6.67% of my available capital on this bet. If my estimation of the minimum probability of winning was right (and I am always very conservative in my guesses so I usually do well at this) then this was a great bet.
Even by winning such a bet just 30% of the time, one could make substantial profits over the course of many bets.
Risk Is A Matter Of Taste
The Kelly Criterion is mathematically optimal for picking risk size per bet but it does have a drawback that many traders like to adjust for.
A feature of it is that it provides a "mirror" probability of losing a given percentage of your capital. When a series of bets are placed using the Criterion it gives the trader a 50% chance of at some time reducing his capital to 50% of the starting amount, a 40% chance or reducing it to 40%, a 10% chance of reducing it to 10% and so on. While he will probably make the losses back if he uses the model correctly this is just too much risk for many traders.
The solution to this is to calculate the risk amount per bet using the Kelly Criterion and then to divide it by a number depending on your risk appetite. The reduction in bet size does not decrease the long run returns linearly. For example, betting at 50% of the suggested amount will still pay the trader 75% of the returns that risking the full Kelly bet amount would have done but with far less volatility.
Why And Where To Use The Kelly Criterion
The Kelly Criterion provides the mathematically optimal balance of risk versus reward. Some traders are more concerned with risk and others with reward.
Betting more than the Kelly percentage is never optimal and will probably lead to long term depletion of capital and many traders are most comfortable at 50% or even 33.33% of the Kelly bet size. I am a fairly aggressive trader so choose to bet 100% of the Kelly size relative to the funds in each of my trading accounts.
If you have a tougher time determining the probability of success for each bet you make then Kelly betting is not for you. It is predicated on the ability to pick 'good bets'. You may however be interested in considering risk diversification and bet size in light of a model which does not require such knowledge. If so, see my article here: Beating The Risk Of Ruin.
Kelly betting is best deployed in trading scenarios where the stake and payout are known in advance. My interest in Kelly bet sizes is that the model is perfect for fixed odds financial betting and lends itself perfectly to Binarys, One Touches, No Touches, Time Switches and their respective ranges.
Last edited by a moderator:
