thinking about restarting
My Melancholy Blues - Queen - YouTube
For a few reasons I will wait another month:
1) I want to keep learning to count the cents of all daily expenses, and saving, as I've been doing.
2) I might get a donation from my parents for christmas or similar.
3) I will get the usual extra salary for the end of the year (from my job, normal here in italy).
4) I might find some investor
5) I might benefit from some more math
But after a month, in January, I will be able to resume trading on my own, with a few systems. I don't know if I'll do it, but let's consider the candidate systems anyway:

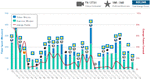
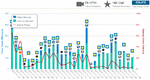
By looking at my scatter plot, I have identified 4 of them, which have a low margin and drawdown, and a high sharpe ratio:

Margin-wise, I'd just need 2000. Drawdown-wise I'd need 5000 to be safe. Those 2000 I'd have right now, but I can't start with just that. I'd need the 5000, and for those, I am regretting the hundreds of lunches/dinners I've had over the last few years. Now I know why everyone was so happy to let me pay for them. That's why I will benefit from some more time spent saving and counting cents. If I can get as far as coming back home on the subway, it will really show me that I've learned the value of money. I hope one day I will not go back to wasting money after learning how precious money is.
All things considered, by coming back on the subway, I would save 220 euros per month. It's not a lot, but it cannot be ignored. And if I don't at least get myself to do that, I will not have the proof that I have learned the value of money, and without that, money management is at risk, because its first requirement is the desire to not lose money. The question to myself is this: how much do i really want to succeed? Do I really care or am I just happy with a regular life? And how much sacrifices am I willing to make to achieve it? Or do I just want to achieve it with intellectual work and no material effort? I might need material effort and learn the value of money.
You know, I often think of robbing a bank, but taking the subway to save a few hundreds never crosses my mind. I admit it might be because I am spoiled. It's easier to fantasize about this than making it happen overnight, which could actually be the case. In the same way I don't fancy walking into interviews or asking anyone for help. All my life my father has made things happen for me (got me jobs, etc.) and he has gotten me used to seeing things happen, without efforts.
Anyway, I will not have 5000 in January (unless I get some money from my parents). And since I don't want to get another loan, nor trade just one system, because it'd be too boring, then I won't resume trading in January. It would be unsafe otherwise.
I wish I could invest in mini-mini-futures, with commissions and spread costs being mini-mini-commissions and mini-mini-spread costs. But it cannot be done. If it could be done I'd invest in... but then I'd really have to figure out the portfolio theory I'm ignoring. Starting small allows me to start without having to worry about portfolio theory, because you can't really do any combinations if you're trading just 4 systems. You either trade them or you don't.
Anyway, I am paying for past mistakes, both with trading and spending money every day on unnecessary things. Let's focus on the future and what I can still do right. I could not find any extra sources of income, and resuming full-time is not a good idea, because the salary doesn't increase by much, and my free time is more important.
All I can focus on right now is doing math, which is like producing capital in my head. And also I can focus on not spending the little money I make. The day I'll take the subway home for one month, it will be a humiliation, but I will also be one step closer to being successful. All it takes is walking down into the subway. I need to learn to count the cents.